Квантовая модель свободных электронов в металле.

Парная ковалентная связь имеет два предельных варианта: ионная и металлическая связь. При металлической связи электронные пары не являются собственностью двух соседних атомов, но принадлежат всем ионам решетки. Иными словами образуется гигантское электронное облако гигантской молекулы – кристалла. Силы отталкивания между электронами компенсируются силами притяжения к ионам кристаллической решетки. На рис. 6а изображена плоская модель свободных электронов в металле.

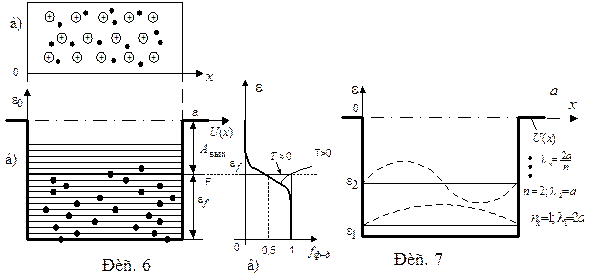
При нормальных условиях электроны свободного электронного газа не могут выйти за пределы металлического образца, т.е. они находятся в прямоугольной потенциальной яме U(x) (рис. 6б) .

Квантование энергии электрона в потенциальной яме показано на рис.7 для одномерного случая. Движению электрона в потенциальной яме можно поставить в соответствие стоячие волны Де-Бройля, причем волновые функции электронов на границах ямы обращаются в нуль.

Условие существования стоячих волн Де-Бройля

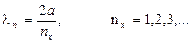(2)

где l_n – длина волны, n_x – квантовое число, a – ширина потенциальной ямы.

Разрешенные значения импульса и энергии электрона в потенциальной яме.

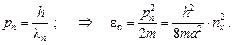(3)

Таким образом, квантование энергии электрона в потенциальной яме обусловлено его волновыми свойствами.

В общем случае трех измерений состояние электрона в трехмерной прямоугольной потенциальной яме определяется четырьмя квантовыми числами n_x, n_y, n_z и s.

n² = n_x² + n_y² + n_z²; n_x, n_y, n_z = 0,1,2,3,… (4)

s = + Ѕ – спиновое квантовое число.

Комбинация n_x = n_y = n_z =0 не имеет физического смысла.

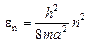. (5)

Работа выхода A_вых представляет собой разность между энергией электрона, покоящегося в вакууме на бесконечно большом расстоянии от кристалла, и уровнем Ферми .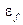

2.2. Принцип Паули. Распределения Максвелла-Больцмана,
Ферми-Дирака и Бозе-Эйнштейна

Рассмотрим некоторые общие закономерности поведения электронов в твердых телах. Важнейшим и наиболее фундаментальным правилом является принцип Паули, согласно которому в квантовой системе не может быть двух электронов, обладающих одинаковым значением четырех квантовых чисел (4). Иными словами, в одном и том же состоянии не могут находиться одновременно два электрона.

Статистическая теория, в основе которой лежит принцип Паули, называется статистикой Ферми-Дирака. Центральным понятием статистического метода является функция распределения. Функция распределения Ферми 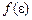дает вероятность того, что состояние с энергией 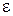занято. Коль скоро известен точный вид функции Ферми для данной системы электронов, можно найти и вероятность заполнения любого ее состояния.

Для должного понимания явления электропроводности полупроводников используют три функции распределения:

a) Максвелла-Больцмана 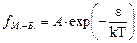; (6)

б) Ферми-Дирака 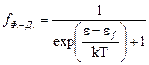; (7)

в) Бозе-Эйнштейна 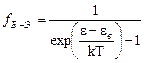. (8)

Каждая функция распределения показывает, какую долю общего числа частиц составляют частицы с заданной энергией 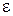. Вид этих функций различен, так как весьма различны основные свойства частиц, к системам которых они относятся. Распределение Максвелла-Больцмана применимо в тех случаях, когда частицы системы можно считать классическими (и различимыми). Распределения Ферми-Дирака и Бозе-Эйнштейна учитывают тождественность частиц. При этом первое из них описывает системы частиц, подчиняющиеся принципу Паули, т.е. системы электронов, протонов и нейтронов, а второе применяется к системам фононов, фотонов и элементарных частиц с нулевым или целым спином.

Замечательно, что вид функции Ферми-Дирака не зависит от свойств той или иной конкретной системы, а зависит лишь от температуры. Свойства системы определяют параметр 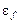– уровень Ферми, который показывает, как нужно располагать функцию Ферми относительно энергетических уровней системы (см. рис. 6).

Параметр 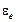играет аналогичную роль в статистике Бозе. В случае фононов и фотонов, число которых может и не сохраняться, .

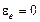Перечислим важнейшие свойства уровня Ферми :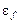

1. С уровнем Ферми совпадает энергетический уровень, вероятность заполнения которого равна половине. При температуре в области абсолютного нуля уровень Ферми разделяет свободные и заполненные энергетические уровни (рис. 6в).

2. Уровень Ферми представляет собой химический потенциал электронов данной системы (в расчете на один электрон). Поэтому условием равновесия двух электронных проводников (безразлично, металлов или полупроводников) является равенство их уровней Ферми.

3. Уровень Ферми определяется из условия, что, независимо от распределения по уровням, полное число электронов в кристалле должно оставаться неизменным. Это требование непосредственно связано с условием нейтральности полупроводника в целом. Это условие обычно и используется для вычисления уровня Ферми и тем самым, числа свободных электронов и дырок.

На рис.6 энергия уровня Ферми отсчитывается от дна потенциальной ямы. Расчет дает для 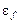при температуре в области абсолютного нуля для металлов

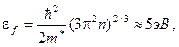(9)

где m^* – эффективная масса электрона. Она определяется следующим выражением

.

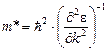Эффективная масса m^* в отличие от обыкновенной массы m не характеризует ни энергию, ни инерциальные свойства, а учитывает лишь взаимодействие ускоряемого электрона с решеткой. Эффективная масса электрона может быть как меньше, так и больше массы электрона и даже отрицательной. Эффективная масса электрона зависит от направления его движения в кристалле и в связи с анизотропией свойств кристаллов является тензором, в общем случае элементы которого соответственно равны

.

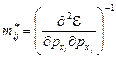У свободного электрона, на который не действуют силы со стороны решетки 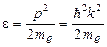, отсюда 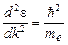; m*=m_e , то есть эффективная масса равна обычной .

Введя понятие эффективной массы, можно считать электрон свободным и описывать его движение по тем же формулам, что и для свободного электрона , не учитывая влияние периодического поля кристалла. Теоретический расчет эффективной массы очень сложен и поэтому, как правило, ее определяют экспериментально.

Энергетический интервал от уровня Ферми до верхнего края потенциальной ямы равен работе выхода электрона с поверхности проводника. В частности, для вольфрама А_вых = 4,5 эВ.

Функция распределения Ферми-Дирака изображена на рис 6в. Действие принципа Паули проявляется в том, что при очень низких температурах функция Ферми-Дирака равна единице вплоть до энергии 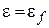, после чего она скачком падает до нуля. Это значит, что все состояния с энергиями ниже уровня Ферми заняты, а все состояния с более высокими энергиями свободны. При более высоких температурах функция Ферми убывает хотя и быстро, но уже непрерывно.

При условии 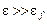единицей в знаменателе выражения (7) можно пренебречь. Следовательно, в области “хвоста” функция Ферми-Дирака приближается к функции Максвелла-Больцмана

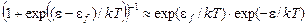. (10)

Этот вывод весьма важен для теории полупроводников.