Концентрация носителей заряда в невырожденном полупроводнике n-типа

На рис. 11 представлена схема энергетических уровней в объеме полупроводника. Следует подчеркнуть, что наличие запрещенных зон энергии непосредственно не влияет на распределение электронов. Это значит, что при заданном положении уровня Ферми заполнение электронами тех или иных состояний в зоне проводимости совершенно не зависит от наличия под зоной проводимости запрещенного участка.

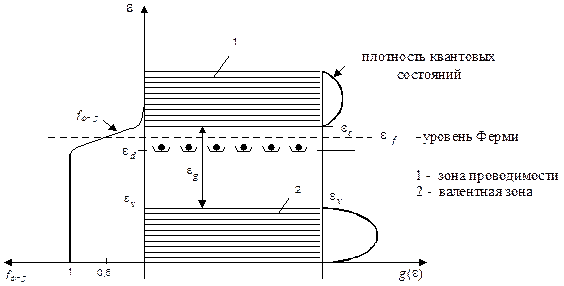
Рис.11.

В нормальном состоянии валентная зона целиком заполнена, а зона проводимости – пуста. Электроны в зону проводимости и дырки в валентную зону доставляются примесью – соответственно донорной и акцепторной. Кроме того, при достаточно высоких температурах электроны могут возбуждаться непосредственно из валентной зоны в зону проводимости, давая начало собственной проводимости. Заметим, что механизмы возбуждения могут быть самыми различными: тепловое возбуждение, фотовозбуждение и др.

В настоящем параграфе мы рассмотрим лишь полупроводник n-типа (примесь донорного типа). Допустим, что все донорные уровни характеризуются одной и той же энергией – 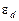. Обозначим концентрацию примесных центров через N_d.

Никакие расчеты статистического характера невозможны до тех пор, пока неизвестно, сколько состояний соответствует данной энергии. Плотность квантовых состояний соответствует данной энергии. Плотность квантовых состояний 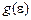– это количество состояний на единичный интервал энергии. Функция 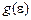для полупроводника представлена в правой части рис.11. Она состоит из трех частей:

1). У краев зоны проводимости и валентной зоны 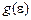меняется как 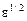и дается формулой

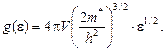(24)

2). В запрещенной зоне 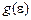отлична от нуля только при энергии, соответствующей примесному уровню.

3). При 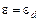плотность состояний 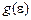ведет себя как 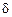-функция

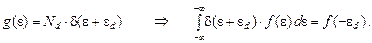(25)

Концентрация электронов в зоне проводимости вычисляется интегрированием (метод Гиббса)

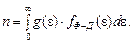(26)

Опуская весьма громоздкую процедуру определения уровня Ферми и вычисления интеграла, запишем окончательное выражение для концентрации свободных электронов

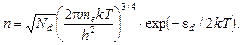(27)

Экспонента в (27) появилась потому, что при рассмотрении полупроводника n-типа мы исходим из функции распределения Ферми, но в конце-концов аппроксимировали ее (с большой точностью) функцией Больцмана (см. формулу (10)). Действительно, несмотря на то, что к электронам полупроводника в принципе необходимо применять статистику Ферми, большая часть электронов, участвующих в электропроводности, находится на уровнях, отстоящих от уровня Ферми на значительном (по сравнению с kT) расстоянии и потому подчиняется распределению Максвелла-Больцмана. Это соответствует относительно слабой ионизации примесей при достаточно низких температурах, когда уровень Ферми лежит в запрещенной зоне примерно посредине между уровням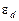и и 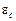(см. рис. 11).

При этих условиях из формулы (27) следует, что концентрация свободных электронов растет лишь как корень квадратный из концентрации примесных центров. При достаточно высоких температурах все электроны, естественно, переходят с донорных уровней в зону проводимости. Число свободных электронов при этом равно 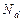. Соответствующий интервал температур носит название области насыщения.

Из формулы (27) следует, что с ростом температуры величина 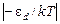уменьшается, при этом экспонента отрицательного аргумента увеличивается, т.е. концентрация электронов проводимости растет по закону, близкому к экспоненциальному.