Соотношение Эйнштейна для коэффициентов диффузии и электропроводности. Вывод формулы для электропроводимости

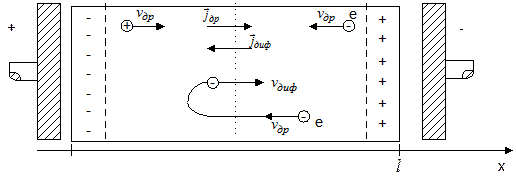
Рис. 10. Диффузия и дрейф заряда в полупроводнике.

Поместим полупроводниковый образец между обкладками плоского конденсатора. В начальный момент времени после зарядки конденсатора в полупроводнике возникнет дрейфовый поток электронов и дырок под действием внешнего электрического поля. В результате этого на концах проводника с координатами 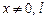возникнут области индуцированного пространственного заряда определенной толщины, которые создадут свое внутреннее поле в объеме полупроводника. Накопление индуцированного заряда происходит до тех пор, пока внутреннее индуцированное поле не скомпенсирует внешнее электрическое поле конденсатора, благодаря чему суммарное электрическое поле внутри полупроводника будет равно нулю. Рассмотренное явление получило название эффекта поля.

В состоянии равновесия в полупроводнике устанавливается некоторый градиент концентрации электронов вдоль оси x. Распределение концентрации электронов вдоль оси x соответствует распределению Больцмана:

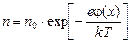. (15)

При наличии градиента концентрации возникает диффузионный ток, определяемый законом Фика

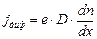. (16)

Дрейфовый ток определяется законом Ома

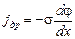. (17)

Состояние равновесия характеризуется равенством диффузионного и дрейфового токов

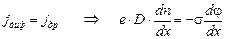. (18)

С другой стороны из распределения Больцмана (15) имеем

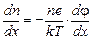. (19)

Подставляя (19) в (18), получаем

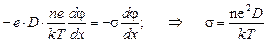– соотношение Эйнштейна. (20)

Согласно (12) коэффициент диффузии

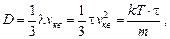(21)

где использованы формулы 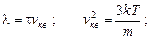(22)

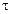– время релаксации.

Подставляя (21) в (20), получаем формулу для электропроводимости

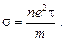(23)

Такой же результат следует из квантовой теории, однако в (23) масса электрона заменяется его эффективной массой m^*.