Время жизни неравновесных носителей заряда
Рассмотрим собственный полупроводник, находящийся в состоянии термодинамического равновесия. При достаточно высоких температурах наблюдается переброс электронов непосредственно из валентной зоны в зону проводимости.
Свободные носители заряда, возникающие в результате тепловой генерации и находящиеся в термодинамическом равновесии с кристаллической решеткой, называют равновесными.
Одновременно с генерацией свободных носителей заряда идет процесс рекомбинации: электроны возвращаются в свободные состояния в валентной зоне, в результате чего исчезают свободный электрон и свободная дырка.
В условиях термодинамического равновесия процессы генерации и рекомбинации взаимно уравновешиваются. Введем обозначения:
G0 – число генерируемых электронно-дырочных пар в единице объема кристалла за одну секунду.
R0 – число рекомбинирующих электронно-дырочных пар в единице объема кристалла за одну секунду.
Вероятность рекомбинации пропорциональна произведению концентраций свободных носителей заряда, то есть
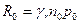 , (6)
, (6)
где 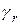 - коэффициент рекомбинации.
- коэффициент рекомбинации.
Для равновесного состояния полупроводника справедливо равенство
G0 = R0 ,(7)
которое является выражением принципа детального равновесия.
Помимо тепловой генерации имеются другие механизмы, приводящие к возникновению свободных носителей заряда. Например, они могут образоваться в результате облучения полупроводника светом, разрыва валентных связей в сильных электрических полях или инжекции с помощью p-n–перехода. Во всех этих случаях возникает некоторая концентрация электронов n и дырок p, которая отличается от термодинамически равновесной.
Подвижные носители заряда, не находящиеся в термодинамическом равновесии как по концентрации, так и по энергетическому распределению, являются неравновесными носителями заряда, а их концентрацию n, p называют неравновесной. Избыток неравновесной концентрации носителей заряда 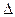 n,
n, 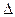 p в полупроводнике по сравнению с равновесной n0 , p0 принято называть избыточной концентрацией носителей заряда.
p в полупроводнике по сравнению с равновесной n0 , p0 принято называть избыточной концентрацией носителей заряда.
При оптической генерации носители заряда могут иметь кинетическую энергию, значительно превышающую среднюю тепловую энергию равновесных частиц. В результате рассеяния на дефектах кристаллической решетки носители заряда довольно быстро передают ей свою избыточную энергию.
Произведем следующий расчет. Допустим, что энергия электронов, генерированных светом, в зоне проводимости составляла 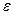 = 1эВ. Из теории столкновений следует, что при рассеянии на длинноволновых акустических фононах электроны за одно столкновение будут передавать решетке энергию
= 1эВ. Из теории столкновений следует, что при рассеянии на длинноволновых акустических фононах электроны за одно столкновение будут передавать решетке энергию 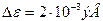 . Таким образом, для рассеяния своей избыточной энергии избыточные электроны должны совершить
. Таким образом, для рассеяния своей избыточной энергии избыточные электроны должны совершить 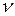 столкновений с акустическими фононами
столкновений с акустическими фононами
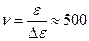 столкновений. (8)
столкновений. (8)
Далее учтем, что средняя длина свободного пробега электронов 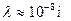 , а их тепловая скорость при комнатной температуре составляет
, а их тепловая скорость при комнатной температуре составляет 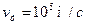 . Следовательно, среднее время между двумя столкновениями
. Следовательно, среднее время между двумя столкновениями
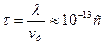 (9)
(9)
и через время 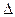 t избыточные электроны приобретут температуру кристаллической решетки
t избыточные электроны приобретут температуру кристаллической решетки
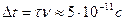 . (10)
. (10)
Это очень малый промежуток времени, поэтому распределение по энергиям неравновесных и равновесных носителей заряда будет одинаковым. Соответственно неравновесные дырки, рассеивая избыточную энергию, «поднимаются» к верхнему краю валентной зоны.
Электроны и дырки, генерированные светом, являются неравновесными по причине того, что они создают избыточную неравновесную концентрацию носителей при данной температуре.
Общая концентрация электронов и дырок будет равна соответственно
n = n0 + 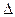 n ; p = p0 +
n ; p = p0 + 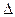 p. (11)
p. (11)
Рассмотрим полупроводник, в котором оптической генерацией создается некоторая концентрация электронов и дырок. Генерацию носителей заряда, при которой в результате возбуждения возникают пары – электрон и дырка, будем называть биполярной генерацией. В этом случае поглощение кванта света сопровождается разрывом ковалентной связи и количество генерируемых избыточных электронов и дырок одинаково:
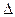 n =
n = 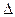 p . (12)
p . (12)
Параллельно с процессом генерации идет процесс рекомбинации, и в стационарном состоянии число электронов и дырок, возбуждаемых за единицу времени в результате разрыва ковалентных связей, равно числу электронов и дырок, рекомбинирующих за это же время. Поскольку неравновесные носители заряда через очень малое время (10) становятся физически неотличимыми по энергии от равновесных, можно считать, что они имеют тот же коэффициент рекомбинации 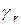 , что и равновесные носители заряда.
, что и равновесные носители заряда.
После выключения возбуждающего света концентрации электронов и дырок уменьшаются в результате рекомбинации. Найдем закон уменьшения концентрации избыточных электронов и дырок после прекращения возбуждения. Для этого составим соответствующее дифференциальное уравнение и решим его.
Скорость убывания числа свободных электронов и дырок определяется разность скорость рекомбинации к тепловой генерации
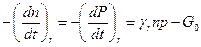 . (13)
. (13)
Принимая во внимание (6). (7), (11) и (12), уравнение (13) можно переписать следующим образом
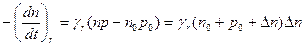 . (14)
. (14)
Рассмотрим случай малого уровня возбуждения, когда выполняется условие
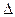 n << (n0 + p0) . (15)
n << (n0 + p0) . (15)
При этом условии слагаемым 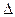 n в правой части (14) можно пренебречь и уравнение (14) принимает вид
n в правой части (14) можно пренебречь и уравнение (14) принимает вид
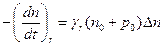 . (16)
. (16)
Введем обозначение
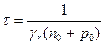 (17)
(17)
и учтем, что
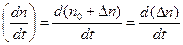 . (18)
. (18)
В итоге из (16) получаем простое дифференциальное уравнение для определения закона уменьшения концентрации избыточных носителей заряда.
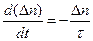 (19)
(19)
Разделив переменные, легко получаем решение уравнения (19)
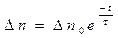 , (20)
, (20)
где 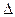 n0 – избыточная концентрация электронов в момент выключения возбуждающего света.
n0 – избыточная концентрация электронов в момент выключения возбуждающего света.
Вывод: в случае малого уровня биполярной генерации избыточная концентрация электронов и дырок после прекращения возбуждения уменьшается по экспоненциальному закону и за время 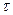 количество их в результате рекомбинации убывает в е раз. Следовательно,
количество их в результате рекомбинации убывает в е раз. Следовательно, 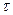 представляет собой среднее время существования избыточной концентрации электронов и дырок, и поэтому его называют временем жизни неравновесных носителей заряда. Для собственного полупроводника скорости убывания числа электронов и дырок равны и значение
представляет собой среднее время существования избыточной концентрации электронов и дырок, и поэтому его называют временем жизни неравновесных носителей заряда. Для собственного полупроводника скорости убывания числа электронов и дырок равны и значение 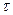 определяет время жизни электронно-дырочных пар.
определяет время жизни электронно-дырочных пар.
Значение объемного времени жизни неравновесных носителей заряда в зависимости от типа полупроводникового материала и от степени его чистоты может уменьшаться в очень широких пределах – от 10-8 до 10-2 см.
В случае большого уровня биполярного возбуждения
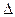 n >> (n0 +p0) (21)
n >> (n0 +p0) (21)
из (14) находим
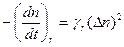 , (22)
, (22)
т.е. скорость рекомбинации зависит от 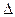 n по квадратичному закону.
n по квадратичному закону.
Разделяя переменные, получим
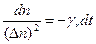 . (23)
. (23)
Отсюда следует
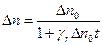 . (24)
. (24)
Выражение (24) говорит о том, что при квадратичной рекомбинации избыточная концентрация носителей заряда уменьшается по гиперболическому закону.
Фотопроводимость
Пусть на поверхность полупроводника нормально падает свет интенсивностью I (рис. 3).
Под интенсивностью света будем понимать количество энергии света, падающей на единицу поверхности за одну секунду. Пусть свет полностью поглощается полупроводником в слое толщиной dx (рис. 3).
Количество световой энергии, поглощаемой в единицу времени в единице объема вещества, равно
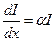 , (25)
, (25)
где 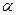 – коэффициент поглощения света.
– коэффициент поглощения света.
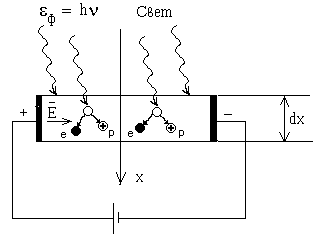
Рис. 3. Проводимость полупроводника под действием света.
Количество избыточных электронов и дырок, образующих под действием света в единице объема в единицу времени (скорость генерации)
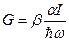 , (26)
, (26)
где 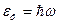 – энергия фотона.
– энергия фотона.
Коэффициент 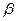 называется квантовым выходом фотоэффекта и определяет число пар носителей, образующихся в среднем на один поглощенный фотон.
называется квантовым выходом фотоэффекта и определяет число пар носителей, образующихся в среднем на один поглощенный фотон.
Пусть 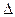 n и
n и 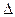 p есть концентрации избыточных (неравновесных) электронов и дырок, образовавшихся в результате внутреннего фотоэффекта. Следовательно, полная проводимость полупроводника (в пределах слоя толщиной dx) определяется равновесными носителями заряда n0 и р0 и фотоносителями
p есть концентрации избыточных (неравновесных) электронов и дырок, образовавшихся в результате внутреннего фотоэффекта. Следовательно, полная проводимость полупроводника (в пределах слоя толщиной dx) определяется равновесными носителями заряда n0 и р0 и фотоносителями 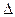 n и
n и 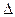 p.
p.
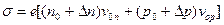 , (27)
, (27)
где von и vop – подвижности электронов и дырок.
Темновая электропроводимость полупроводника
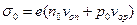 . (28)
. (28)
Отсюда фотопроводимость полупроводника, обусловленная непосредственным действием излучения, есть
 |
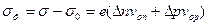 . (29)
. (29)
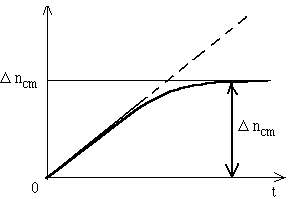
Рис. 4. Зависимость концентрации избыточных носителей заряда от времени в полупроводнике при постоянном освещении.
Однако сразу после начала освещения фотопроводимость полупроводника не достигает максимального значения, ибо по мере увеличения концентрации неравновесных носителей заряда нарастает процесс рекомбинации. Поскольку скорость генерации неравновесных носителей остается постоянной при неизменной интенсивности света, то через некоторый промежуток времени интенсивность рекомендации достигает интенсивности генерации и установиться стационарное состояние, характеризующееся постоянным значением концентрации фотоносителей заряда  nст и
nст и  pст (см. рис. 4).
pст (см. рис. 4).
Из (26) следует
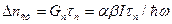 ; (30)
; (30)
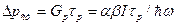 . (31)
. (31)
Стационарная фотопроводимость равна согласно (25)
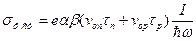 . (32)
. (32)
Если один из членов в скобках выражения (32) значительно больше другого (за счет разницы в значениях подвижности или времени жизни электронов и дырок), то фотопроводимость определяется носителями заряда одного знака и её называют монополярной. В этом случае
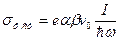 . (33)
. (33)
Выражение для стационарного значения и плотности фототока во внешнем электрическом поле напряженностью Е (рис. 3):
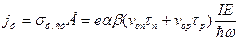 (34)
(34)
Дата добавления: 2015-12-16; просмотров: 4393;
