ЛЕКЦИЯ 2. Математическая модель изображений

Принципы компьютерной обработки изображений

Изображения играют в нашей жизни огромную роль. В начале развития науки и техники существовал только один способ регистрации изображений – их зарисовка. При перерисовке изображения явления неминуемо возникали неточности. Это сильно затрудняло продвижение научных исследований.

В наше время все большую роль в научных исследованиях и повседневной жизни занимают изображения, регистрируемые на фотоаппарат, видеокамеру и т.д.

Изображения, сформированные различными оптико-электронными системами и зарегистрированные с помощью разнообразных приёмников искажаются действием помех различного характера. Искажения изображения вносятся всеми компонентами изображающего прибора, начиная с осветительной системой (например, неравномерность освещенности предмета). Искажения, которые вносит оптическая система, известны еще на этапе её проектирования и называются аберрации. Искажения, которые вносят электронные приёмники излучения, например ПЗС-матрицы, называются электронный шум. Помехи затрудняет визуальный анализ изображения и его автоматическую обработку.

Ослабление действия помех достигается фильтрацией. При фильтрации яркость (сигнал) каждой точки исходного изображения, искаженного помехой, заменяется некоторым другим значением яркости, которое признается в наименьшей степени искаженным помехой. Для выполнения фильтрации необходимо выработать принципы таких преобразований, которые основываются на том, что интенсивность изображения изменяется по пространственным координатам медленнее, чем функция помех. В других случаях, наоборот, признаком полезного сигнала являются резкие перепады яркости.

Цифровая обработка и распознавание изображений - одно из интенсивно развиваемых направлений исследования.

Компьютерная обработка изображений предполагает обработку цифровых изображений с помощью компьютеров или специализированных устройств, построенных на цифровых сигнальных процессорах.

При этом под обработкой изображений понимается не только улучшение зрительного восприятия изображений, но и классификация объектов, выполняемая при анализе изображений. В 60-е годы прошлого века получила развитие особая наука об изображениях – «иконика», которая посвящена исследованиям общих свойств изображений, целей и задач их преобразования, обработки и воспроизведения, распознавания графических образов. Термин «иконика» происходит от греческого «eikon», что означает изображение, образ. Сегодня под ним понимают «создание и обработку изображений с помощью ЭВМ, что совпадает с понятием компьютерной обработки изображений.

В компьютере изображение хранится на жестком диске в виде отдельного файла графического формата. Самым распространенным графическим форматом представления изображения в компьютере является BMP. В этом формате изображение хранится без потерь и искажений, которые являются результатом сжатия изображений (как например графический формат JPEG) в виде битовой матрицы. Минимальный неделимый элемент битовой матрицы – пиксель. Совокупность пикселей образует изображение [7].

Пиксель характеризуется определенным цветом и определенной яркостью. Воздействуя на эти характеристики каждого пикселя – элемента изображения, можно изменять качественные характеристики изображения в зависимости от поставленной задачи.

В методах фильтрации при оценке реального сигнала в некоторой точке кадра принимают во внимание некоторое множество (окрестность) соседних точек, воспользовавшись определенной похожестью сигнала в этих точках. Понятие окрестности является достаточно условным. Окрестность может быть образована лишь ближайшими по кадру соседями, но могут быть окрестности, содержащие достаточно много и достаточно сильно удаленных точек кадра. В этом случае, степень влияния (вес) далеких и близких точек на решения, принимаемые фильтром в данной точке кадра, будет совершенно различной. Таким образом, идеология фильтрации основывается на рациональном использовании данных как из рабочей точки, так и из ее окрестности.

При решении задач фильтрации используют вероятностные модели изображения и помехи, и применяют статистические критерии оптимальности. Это связано со случайным характером помехи и стремлением получить минимальное в среднем отличие результата обработки от идеального сигнала. Многообразие методов и алгоритмов фильтрации связано с большим разнообразием математических моделей сигналов и помех, а также различными критериями оптимальности.

Однако, несмотря на их множество можно объединить методы фильтрации изображений в несколько групп (рисунок 1.1).

Точечные методы. В этом виде обработки применяются алгоритмы, которые изменяют значения яркости элементов изображения исходя из исходных значений яркости этих элементов и их положения в битовой матрице изображения

Гистограммные методы. В этой группе методов фильтрация осуществляется исходя из статистических характеристик изображения. Могут выполняться эквализация гистограммы или формирование заданной гистограммы.

Методы фильтрации

Рисунок 1 – Классификация методов фильтрации

Пространственная обработка изображений. В этом виде обработки применяются алгоритмы, которые изменяют значения яркости элементов изображения, основываясь не только на значении яркости изменяемого элемента, но и элементов вокруг него. При этом учитываются пространственные статистические характеристики изображения.

Частотные методы фильтрации. В данном случае обработка производится в частотной (спектральной) области. В некоторых случаях эти методы позволяют отфильтровать изображения намного проще, чем пространственные (например, если на изображении присутствуют шумы с частотой, значительно отличающейся от частот на изображении).

Следует отметить, что данные методы обработки сигналов могут применятся как по отдельности, так и, в совокупности – последовательно. Но надо учитывать, что конечный результат сильно зависит от порядка применения различных методов.

Для определенности необходимо уточнить некоторые определения. Пространственная разрешающая способность изображения — это число выборок, используемых для описания изображения. Чем выше пространственная разрешающая способность, тем большее количество единичных элементов в изображении (пикселей) приходится на единицу площади, тем выше качество изображения. Яркость изображения — это общее значение уровней, используемых для того, чтобы выразить значение интенсивности элементов в изображении. Яркостное изображение связано с числом бит, используемых для хранения каждого элемента изображения. Под фильтрацией изображений будем понимать любые методы обработки изображений, направленные на изменение яркостных, пространственных, статистических, частотных характеристик изображения с целью выделить какие-либо особенности изучаемой картины.

Области применения цифровой обработкив настоящее время значительно расширяются, вытесняя аналоговые методы обработки сигналов изображений. Методы цифровой обработки широко применяются в промышленности, искусстве, медицине, космосе. Они применяются при управлении процессами, автоматизации обнаружения и сопровождения объектов, распознавании образов и во многих других приложениях.

Цифровая передача изображений с космических аппаратов, цифровые каналы передачи сигналов изображений требуют обеспечения передачи все больших потоков информации. Если при передаче цифрового сигнала цветного телевидения необходимо передавать потоки порядка 216 Мбит/с, то для передачи телевидения высокой четкости скорость передачи должна составлять порядка 1 Гбит/c. Формирование изображений, улучшение качества и автоматизация обработки медицинских изображений, включая изображения, создаваемые электронными микроскопами, рентгеновскими аппаратами, томографами и т.д., являются предметом исследования и разработки. Сегодня в медицинской технике широко применяются системы формирования изображения, его преобразования в цифровую форму, визуализация и документирование путем введения в компьютер изображений с помощью специализированных устройств захвата видео.

Автоматический анализ в системах дистанционного наблюдения широко применяется при анализе местности, в лесном хозяйстве, например, для автоматического подсчета площади вырубок, в сельском хозяйстве для наблюдения за созреванием урожая, при разведке, в системах противопожарной безопасности. Контроль качества производимой продукции выполняется благодаря автоматическим методам анализа сцен.

Компьютерная обработка изображений применяется в задачах экспертизы живописи неразрушающими методами. Для восстановления старых фильмов применяются методы автоматической компенсации дефектов видеоматериала, полученного после преобразования киноизображения в видео.

Сегодня трудно представить область деятельности, в которой можно обойтись без компьютерной обработки изображений. Интернет, сотовый телефон, видеокамера, фотоаппарат, сканер, принтер, так прочно вошедшие в наш быт, – немыслимы без компьютерной обработки изображений.

При компьютерной обработке изображений решается широкий круг задач, таких как улучшение качества изображений; измерение параметров; спектральный анализ многомерных сигналов; распознавание изображений; сжатие изображений.

Устройства формирования изображений получили широкое распространение и применение в самых различных областях науки, техники, промышленности, медицине, биологии и др. Они являются неотъемлемыми компонентами систем и устройств, применяемых в фотокинотехнике, телевидении, системах технического зрения: дневного, ночного и теплового видения, при дистанционном зондировании Земли. Назначение этих систем предполагает решение комплекса технических и научных задач, требующих синтеза и анализа методов обработки, бинаризации, классификации изображений. Развитие микроэлектроники, переход от аналоговой формы сигналов к цифровой позволяют расширить палитру и повысить сложность применяемых алгоритмов для решения поставленных задач.

ЛЕКЦИЯ 2. Математическая модель изображений

Компьютерная обработка изображений возможна после преобразования сигнала изображения из непрерывной формы в цифровую форму. Эффективность обработки зависит от адекватности модели, описывающей изображение, необходимой для разработки алгоритмов обработки. При этом необходимо учитывать влияние передающей и приемной систем и канала связи на сигнал изображения. Модель изображения представляет систему функций, описывающих существенные характеристики изображения: функцию яркости, отражающую изменение яркости в плоскости изображения, пространственные спектры и спектральные интенсивности изображений, функции автокорреляции. Канал изображения содержит оптическую систему, оптико – электрический преобразователь, устройство аналого - цифрового преобразования (АЦП) и цифровой обработки сигналов изображения. В общем случае непрерывное изображение может быть представлено функцией пяти аргументов: трех пространственных координат, времени и длины волны электромагнитного излучения. Упрощения модели пространственно - временных сигналов в некотором диапазоне волн f (x, y, z,t,λ) приводят к моделям пространственно - временного сигнала f (x, y,z,t), пространственного сигнала f (x, y, z) , временного сигнала f (t) . Здесь x, y,z – пространственные координаты, t – время, λ – длина волны электромагнитного излучения.

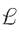Из курса физики хорошо известно понятие оптической системы, осуществляющей преобразование изображений по правилам, определяемым совокупностью используемых в ней оптических элементов и их взаимосвязью.

С математической точки зрения под системой будем понимать правило , ставящее в соответствие входной функции f выходную функцию g. Различают одномерные (1-D) и двумерные (2-D) системы. Одномерные системы преобразуют функции одной переменной:

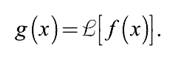
Соответственно двумерные системы преобразуют функции двух переменных:

Оптические системы по сути своей являются двумерными, но в некоторых случаях могут рассматриваться как одномерные. Особое место среди всевозможных систем занимают линейные системы. Система называется линейной, если для нее справедлив принцип суперпозиции (наложения), который заключается в том, что отклик системы на взвешеную сумму двух входных воздействий равен взвешеной сумме откликов на каждое из воздействий, то есть

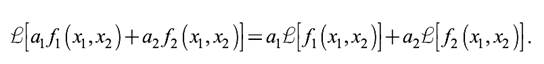
Принцип суперпозиции можно выразить в более общем виде, рассматривая произвольное число K входных воздействий:

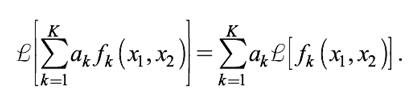
В изучении оптических систем фундаментальную роль играет понятие точечного источника света. Точечный источник обладает бесконечно большой плотностью вероятностей распределения яркости в бесконечно малой пространственной области – в точке:

Такое представление исключительно полезно и допускает ясную физическую трактовку: дельта-функция может быть определена как предел обычной функции, например

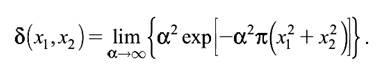(2.1)

Согласно (2.1) дельта-функция может рассматриваться как бесконечно узкая колоколообразная функция, одномерный вариант которой приведен на рисунке 2.1.

Можно также ввести дельта-функцию, расположенную не в начале координат, а в произвольной точке с координатами (x₁, x₂) по формуле

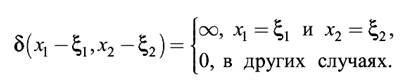
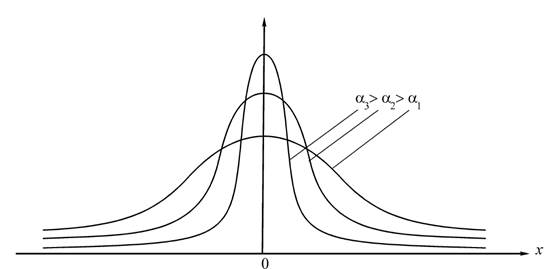
Рисунок 2.1 – Физическая трактовка дельта-функции Дирака

Дельта-функция обладает следующими важными свойствами:

Свойство нормировки:

(2.2)

Физически это означает, что, хотя плотность вероятностей распределения яркости точечного источника бесконечна, энергия его ограничена и равна единице.

Фильтрующее свойство:

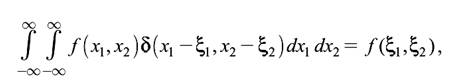(2.3)

где f(x₁, x₂) – произвольная функция двух переменных. Доказательство приведенных свойств выполняются с помощью подстановки в (2.2) и (2.3) выражения (2.1) и раскрытия предела.

Рассмотрим 2-D линейную систему, на вход которой подан сигнал в виде дельта-функции. Реакция системы на дельта-функцию будет разной для различных систем. Она называется импульсным откликом и служит характеристикой 2-D системы. Систему называют пространственно-инвариантной, если ее импульсный отклик зависит от разности координат входной (x₁, x₂) и выходной (x₁, x₂) плоскостей. Для оптической системы, показанной на рисунке 2.2, это означает, что при перемещении точечного источника во входной (предметной) области изображение этого предмета в плоскости наблюдения будет также изменять положение, но сохранять форму.

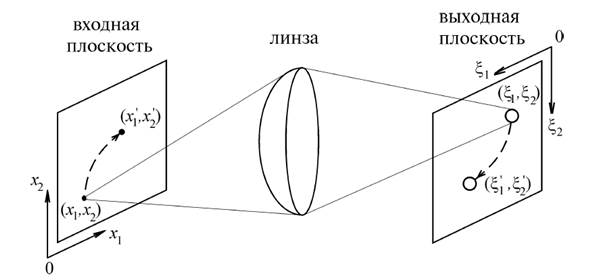
Рисунок 2.2 – Оптическая пространственно-инвариантная система

Для пространственно-инвариантных систем импульсный отклик описывается функцией

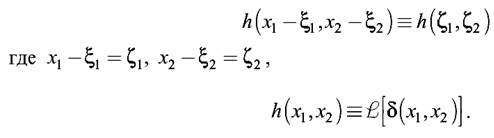
Используя функцию импульсного отклика, можно записать уравнение, связывающее изображения на входе и выходе 2-D линейной оптической системы. Для этого представим входной сигнал f(x₁, x₂) в виде (2.3) и подадим его на вход 2-D системы с характеристикой h(x₁, x₂). Выходной сигнал запишем в виде

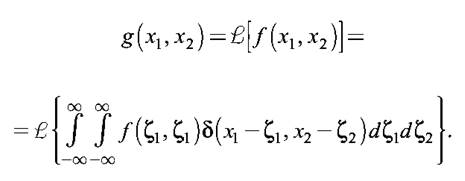(2.4)

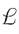Поскольку операция линейна, и операция интегрирования в фигурных скобках (2.4) также линейна, их можно поменять местами и записать, что

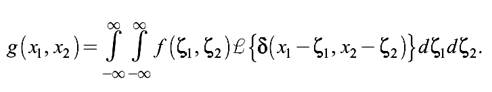
Учитывая, что по определению

окончательно получаем выражение, устанавливающее связь между изображениями во входной и выходной плоскостях линейной системы:

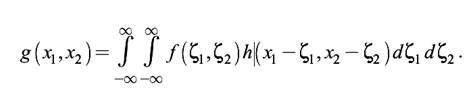(2.5)

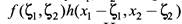Уравнение (2.5) называется интегралом свертки. Из этого уравнения следует, что, зная импульсный отклик оптической системы h(x₁, x₂), можно рассчитать выходное изображение по входному. Процесс свертки иллюстрирует рисунок 2.3. На рисунке 2.3а и 2.3б изображены функция f(x₁, x₂) на входе и импульсный отклик. На рисунке 2.3в показан импульсный отклик при обращении координат, а на рисунке 2.3г – со сдвигом на величину x₁, x₂. На рисунке 2.3д заштрихована область, в которой произведение ,
входящее в подынтегральное выражение (2.5), не равно нулю. Интегрирование по этой области дает величину g(x₁, x₂) для заданных значений координат x₁, x₂. Таким образом, функция g(x₁, x₂) на выходе может быть найдена сканированием входной функции скользящим «окном» – обращенным импульсным откликом, и интегрированием по области, в которой эти функции перекрываются.

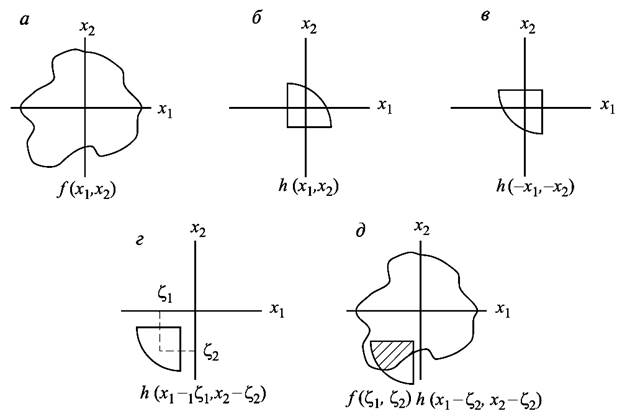
Рисунок 2.3 – Пример двумерной свертки