Среднеквадратичный критерий.

Пусть изображения f(n₁, n₂). и g(n₁, n₂). описываются моделями однородных случайных полей. Мерой соответствия реального изображения идеальному может служить среднее значение квадрата их разности:

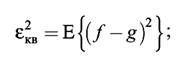
эта величина будет постоянной по всему полю аргументов, поэтому аргументы (одинаковые для f, g) для краткости не указываем.

Если математические ожидания f и g равны, то разность имеет нулевое среднее и величина e_кв² приобретает смысл дисперсии разности (а значение ε_кв – среднеквадратичного отклонения g от f ) двух изображений.

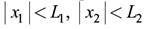Для стационарной модели обычно считается выполненным условие эргодичности, при котором усреднение по ансамблю реализаций может быть заменено на усреднение по одной реализации. Тогда для непрерывных изображений, заданных при

имеем

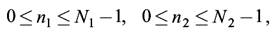
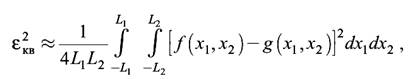(4.1)

а для дискретных, заданных при имеем

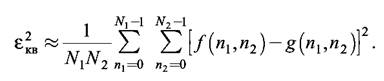(4.2)

Заметим, что в задачах сравнительного анализа вариантов и оптимизации постоянные коэффициенты в (4.1) и (4.2) могут быть отброшены.

Выражения (4.1) и (4.2) позволяют вычислять среднеквадратичную ошибку и для пары произвольных изображений, не обязательно описываемых стационарными полями. Так часто и делается. Однако в этом случае следует иметь в виду, что значение e_кв² будет характеризовать «среднее» качество изображения в целом, а на различных его фрагментах ошибки, в принципе, могут различаться.

Достоинство среднеквадратичного критерия — его простота. При его использовании многие задачи анализа и оптимизации алгоритмов обработки изображений легко решаются аналитически. Поэтому он очень часто применяется.

При обработке изображений следует учитывать, что данный критерий плохо согласуется с критерием субъективного восприятия.