Дискретизация изображения.

Рассмотрим непрерывное изображение – функцию двух пространственных переменных x₁ и x₂ f(x₁, x₂) на ограниченной прямоугольной области (рисунок 3.1).

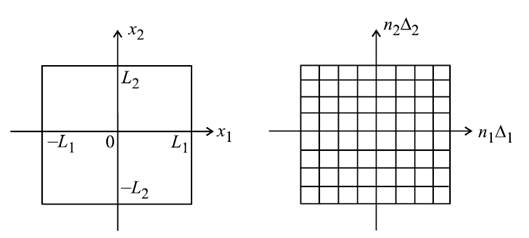
Рисунок 3.1 – Переход от непрерывного изображения к дискретному

Введем понятие шага дискретизации Δ₁ по пространственной переменной x₁ и Δ₂ по переменной x₂. Например, можно представить, что в точках, удаленных друг от друга на расстояние Δ₁ по оси x₁ расположены точечные видеодатчики. Если такие видеодатчики установить по всей прямоугольной области, то изображение окажется заданным на двумерной решетке

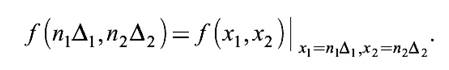
Для сокращения записи обозначим

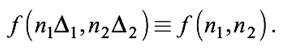
Функция f(n₁, n₂) является функцией двух дискретных переменных и называется двумерной последовательностью. То есть дискретизация изображения по пространственным переменным переводит его в таблицу выборочных значений. Размерность таблицы (число строк и столбцов) определяется геометрическими размерами исходной прямоугольной области и выбором шага дискретизации по формуле

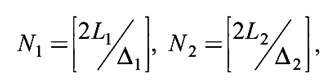
Где квадратные скобки […] обозначают целую часть числа.

Если область определения непрерывного изображения — квадрат L₁ = L₂ = L, и шаг дискретизации выбран одинаковым по осям x₁ и x₂ (Δ₁ = Δ₂ = Δ), то

N₁ = N₂ = N,

и размерность таблицы составляет N².

Элемент таблицы, полученной путем дискретизации изображения, называют «пиксель» или «отсчет». Рассмотрим пиксель f(n₁, n₂). Это число принимает непрерывные значения. Память компьютера способна хранить только дискретные числа. Поэтому для записи в памяти непрерывная величина f должна быть подвергнута аналогово-цифровому преобразованию с шагом Df (см. рисунок 3.2).

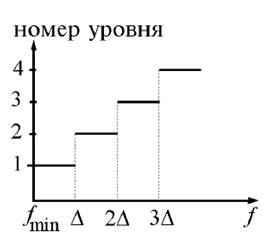
Рисунок 3.2 – Квантование непрерывной величины

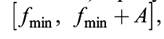Операцию аналого-цифрового преобразования (дискретизации непрерывной величины по уровню) часто называют квантованием. Число уровней квантования, при условии, что значения функции яркости лежат в интервале _____ _ ____ ___, равно

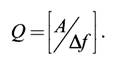
В практических задачах обработки изображений величина Q варьируется в широких пределах от Q = 2 («бинарные» или «черно-белые» изображения) до Q = 210 и более (практически непрерывные значения яркости). Наиболее часто выбираются Q = 28, при этом пиксель изображения кодируется одним байтом цифровых данных. Из всего вышеуказанного делаем вывод, что пиксели, хранящиеся в памяти компьютера, представляют собой результат дискретизации исходного непрерывного изображения по аргументам (координатам?) и по уровням. (Где и сколько, и всё дискретно) Ясно, что шаги дискретизации Δ₁, Δ₂ должны выбираться достаточно малыми, для того, чтобы погрешность дискретизации была незначительна, и цифровое представление сохраняло основную информацию об изображении.

При этом следует помнить, что чем меньше шаг дискретизации и квантования, тем больший объем данных об изображении должен быть записан в память компьютера. Рассмотрим в качестве иллюстрации этого утверждения изображение на слайде размером 50×50 мм, которое вводится в память с помощью цифрового измерителя оптической плотности (микроденситометра). Если при вводе линейное разрешение микроденситометра (шаг дискретизации по пространственным переменным) составляет 100 микрон, то в память записывается двумерный массив пикселей размерности N² = 500×500 = 25∙10⁴. Если же шаг уменьшить до 25 микрон, то размеры массива возрастут в 16 раз и составят N² = 2000×2000 = 4∙10⁶. Используя квантование по 256 уровням, то есть кодируя найденный пиксель байтом, получаем, что в первом случае для записи необходим объем 0,25 мегабайт памяти, а во втором случае 4 мегабайта.