Линеаризация нелинейных дифференциальных уравнений
Реальные САУ имеют в своем составе нелинейные элементы. В некоторых САУ нелинейность носит существенный характер и замена ее линейной зависимостью коренным образом изменяет поведение САУ. Однако в большинстве случаев нелинейность является несущественной и оказывается возможным произвести замену исходных нелинейных уравнений системы линейными, не внося существенных погрешностей. Это позволяет значительно упростить задачу исследования свойств данной САУ.
Под линеаризацией понимается замена нелинейных дифференциальных уравнений линейными уравнениями, которые с достаточной для практики точностью описывают физические процессы в САУ. Признаком, позволяющим произвести линеаризацию уравнений с математической точки зрения, является отсутствие разрывных, неоднозначных или резко изменяющихся характеристик, определяющих зависимость переменных уравнений от различных факторов, т.е. существование производных функций по всем переменным. Физической предпосылкой линеаризации является малая величина отклонений переменных в уравнениях элементов от их установившихся значений в силу самого принципа работы замкнутой автоматической системы, в состав которой эти элементы входят.
Сущность линеаризации в том, что все нелинейные функции одной или нескольких переменных, входящих в уравнение элемента, разлагают в ряд Тейлора в окрестности точки, соответствующей установившемуся режиму, по степеням отклонений. Так, формула Тейлора для нелинейной функции двух переменных x и y имеет следующий вид:
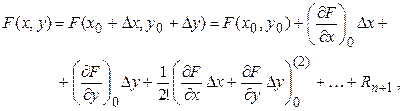 (3.3)
(3.3)
где 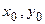 - установившиеся значения переменных;
- установившиеся значения переменных;
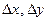 - отклонения переменных от
- отклонения переменных от 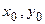 ;
;
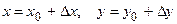 - текущие значения переменных;
- текущие значения переменных;
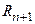 - остаточный член.
- остаточный член.
Индекс “ноль” соответствует условию 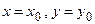 . Показатели степени, в которую возводятся стоящие в скобках выражения, имеют символический смысл, ясный из примера:
. Показатели степени, в которую возводятся стоящие в скобках выражения, имеют символический смысл, ясный из примера:

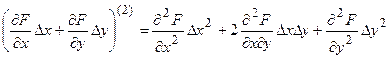 .
.
В формуле (3.3) все частные производные вычисляются в точках с координатами 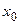 и
и 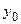 и поэтому являются постоянными величинами. Обычно, если величины отклонений малы, ограничиваются членами первого порядка малости, т.е. пренебрегают остаточным членом ряда. Тогда с точностью до членов второго порядка малости получим формулу Тейлора в виде
и поэтому являются постоянными величинами. Обычно, если величины отклонений малы, ограничиваются членами первого порядка малости, т.е. пренебрегают остаточным членом ряда. Тогда с точностью до членов второго порядка малости получим формулу Тейлора в виде
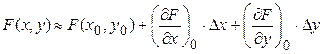 . (3.4)
. (3.4)
Однако при линеаризации уравнений удобнее пользоваться не формулой (3.4), а выражением для приращения функции 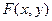 , как более простым. Это приращение определяется разностью между текущим значением функции и ее значением в фиксированной точке с координатами
, как более простым. Это приращение определяется разностью между текущим значением функции и ее значением в фиксированной точке с координатами 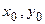 , т.е.
, т.е.
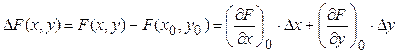 . (3.5)
. (3.5)
Для того чтобы формулу (3.5) применить непосредственно к линеаризации нелинейного уравнения, необходимо из исходных уравнений динамики элементов вычесть уравнения статики. Затем в полученные уравнения подставить выражения для приращения нелинейных функций, определяемых по формуле (3.5).
В итоге получим линеаризованные уравнения в отклонениях, которые являются линейными дифференциальными уравнениями с постоянными коэффициентами и используются для исследования динамических свойств элементов. Неизвестными теперь будут не сами искомые переменные, а их отклонения от установившихся значений.
Рассмотрим порядок линеаризации на конкретном примере. Линеаризовать уравнение:
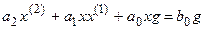
или
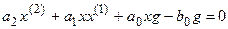 .
.
Обозначим
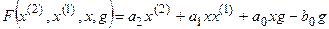 .
.
Запишем линеаризованное уравнение в общем виде:
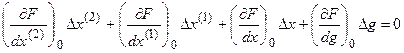 .
.
Определим частные производные, учитывая, что
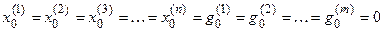 .
.
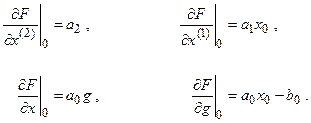
так как 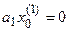 .
.
В соответствии с общим правилом для линеаризации уравнений (3.5) получим уравнение в отклонениях:
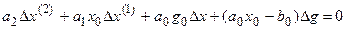 ,
,
или
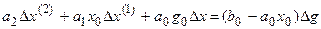 .
.
Приведем уравнение к стандартной форме:
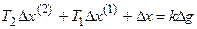 .
.
где
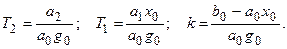
Считая, что отклонения являются переменными относительно их установившихся значений, линеаризованное уравнение можно записать
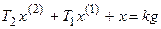 .
.
Дата добавления: 2015-12-11; просмотров: 7870;
