Типовые управляющие и возмущающие воздействия
Любое движение системы автоматического управления вызывается воздействиями, приложенными к системе. Воздействия могут быть управляющими (задающими), которые определяют требуемый закон изменения регулируемой величины, и возмущающими (вредными), которые стремятся нарушить требуемую функциональную связь между регулируемой величиной и задающим воздействием. В общем случае воздействия могут изменяться во времени по закону, который заранее определить невозможно.
Но среди большого количества воздействий можно выбрать наиболее типовое для рассматриваемой системы в данных условиях работы. Изучив движение, возникающее в системе под влиянием данного типового воздействия, можно сделать определенные выводы относительно ее динамических свойств.
Кроме того, любое сложное воздействие можно представить суммой некоторых простых воздействий. Если известны реакции системы на простые воздействия, то, используя принцип суперпозиции, справедливый для линейных систем, можно найти реакцию системы на воздействие сложной формы.
В силу этих причин для анализа и синтеза системы автоматического управления часто используют типовые воздействия. Рассмотрим некоторые из них.
1. Единичная ступенчатая функция 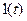 . Единичная ступенчатая функция определяется как воздействие, равное нулю при
. Единичная ступенчатая функция определяется как воздействие, равное нулю при 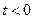 и равное единице, начиная с
и равное единице, начиная с 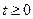 (рис. 4.1,а).
(рис. 4.1,а).
 |
Рис.4.1 а) единичная ступенчатая функция; б) смещенная единичная ступенчатая функция
Таким образом,
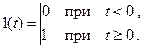 (5.7)
(5.7)
Единичная ступенчатая функция, сдвинутая во времени (смещенная единичная ступенчатая функция), изображена на рис. 4.1,б. Она принимает значение равное единице в момент 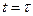 , т.е.
, т.е.
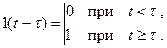 (4.8)
(4.8)
Примерами воздействия, которые можно рассматривать как ступенчатые функции, являются: отключение потребителей энергии от генератора постоянного тока, снабженного регулятором; включение электрической цепи на постоянное напряжение; резкое изменение требуемого направления полета в системе самолет-автопилот и т.д.
2. Единичная импульсная функция 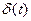 (дельта-функция). На рис. 4.2,а показан импульс длительности Dt, площадь которого равна единице. Если устремить Dt к нулю, то вследствие того, что площадь импульса есть постоянная величина, его высота будет стремиться к бесконечности. Дельта-функция может быть записана так:
(дельта-функция). На рис. 4.2,а показан импульс длительности Dt, площадь которого равна единице. Если устремить Dt к нулю, то вследствие того, что площадь импульса есть постоянная величина, его высота будет стремиться к бесконечности. Дельта-функция может быть записана так:
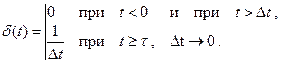 (4.9)
(4.9)
Смещенная единичная импульсная функция изображена на рис.4.2,б. Единичная импульсная функция действует на систему бесконечно малое время, но сообщает ей за это время конечное количество энергии. На практике воздействие d(t) произвести невозможно, однако с небольшими погрешностями в качестве дельта-функции можно принимать кратковременные воздействие, длительность которых существенно меньше длительности переходного процесса в системе. При этом площадь импульса должна быть равна единице.
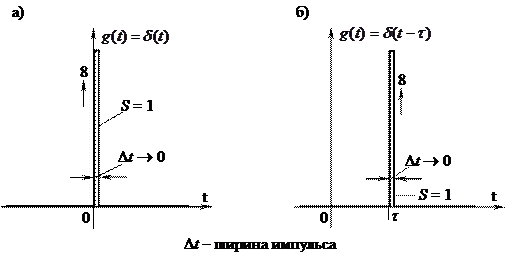 |
Рис. 4.2 а - единичная импульсная функция; б - смещенная единичная импульсная функция
В том случае, когда площадь импульса не равна единице, считают, что воздействие равно 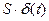 , где S – площадь импульса.
, где S – площадь импульса.
Введение Дираком понятия дельта-функция существенно расширяет возможности теоретического исследования систем. Воздействия типа единичной импульсной функции действует, например, на самолет, когда он пролетает перпендикулярно слой атмосферы с большой скоростью ветра. Между единичной ступенчатой функцией 1(t) и единичной импульсной функцией d(t) существует однозначная зависимость:
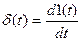 и
и 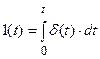 .
.
Следовательно, единичная импульсная функция d(t) является производной от единичной ступенчатой функции.
3. Линейно-меняющийся сигнал. График линейно-меняющегося сигнала представлен на рис. 4.3,б, где а – скорость изменения входного сигнала. Задающее воздействие данного вида характерно для следящих систем.
 |
Рис. 4.3. Типовые воздействия:
а - гармоническое; б - линейно-возрастающее
4. Гармонический сигнал. Гармонический сигнал (рис. 4.3,а) задается в вещественной или комплексной форме. В вещественной форме:
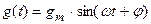 или
или
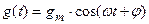 ,
,
где 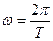 - круговая частота колебаний;
- круговая частота колебаний;
T - период;
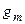 - амплитуда колебаний;
- амплитуда колебаний;
j - начальная фаза.
Иногда бывает удобным задавать гармоническую функцию в комплексной форме
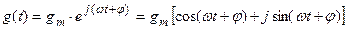 .
.
Дата добавления: 2015-12-11; просмотров: 5643;
