Частотные характеристики САУ

В современной инженерной практике исследования САУ широкое применение получили частотные методы, которые основаны на рассмотрении частотных характеристик отдельных элементов и системы. Если разомкнуть главную обратную связь САУ и подать на вход САУ воздействие синусоидальной формы, то в установившемся режиме на выходе системы получим гармоническую функцию той же частоты, но другой амплитуды и фазы. Анализируя гармонические сигналы на входе и выходе системы, можно установить ее свойства, которые характеризуются частотной функцией

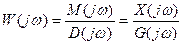. (4.12)

Функция W(jw) называется комплексной передаточной функцией, комплексной частотной характеристикой. Последняя может быть получена путем замены в выражении передаточной функции (4.1) комплексной переменной p на jw:

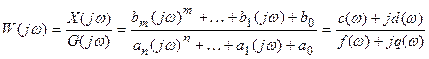, (4.13)

где

;

;

;

.

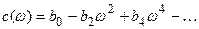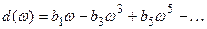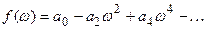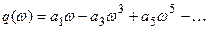Указанная замена равносильна переходу к преобразованию Фурье для дифференциальных уравнений при нулевых начальных условиях. Геометрическое место концов векторов комплексной частотной функции 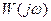при различных частотах представляет собой частотную характеристику, которая называется амплитудно-фазовой частотной характеристикой САУ (рис. 4.6). В дальнейшем как аналитические выражения (4.13) частотных функций, так и их графические представления (рис. 4.6) будем называть соответствующими

Рис. 4.6. Амплитудно-фазовая характеристика САУ

частотными характеристиками. Выражение (4.13) для амплитудно-фазовой характеристики САУ может быть записано в алгебраической форме:

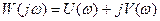
или в показательной форме:

.

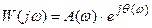Члены U(w) и V(w) алгебраической формы записи W(jw) называются соответственно вещественной и мнимой частотными характеристиками. Они определяются освобождением от мнимого числа в знаменателе W(jw), т.е.:

;

.

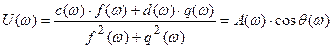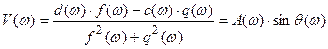Члены A(w) и q(w) показательной формы записи W(jw) называются соответственно амплитудной частотной и фазовой частотной характеристиками и определяются аналитически следующим образом:

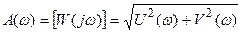; (4.14)

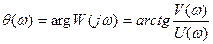. (4.15)

Очевидно, при изменении w будут изменяться величины и модуля A(w), и аргумента q(w) вектора, изображающего комплексную величину W(jw) (рис. 4.6).

Покажем физическую интерпретацию A(w) и q(w). Если на вход устойчивой динамической системы подать гармоническое воздействие

,

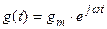то по окончании переходного процесса на ее выходе установятся вынужденные колебания с той же частотой w, но с другой амплитудой и фазой:

,

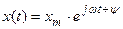где y - разность фаз величин x и g. При этом для одной и той же системы разным значениям w соответствуют определенные величины отношений 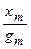и y.

При известных входной и выходной величинах

.

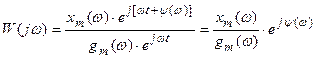Из сравнения правых частей выражений для W(jw) следует, что

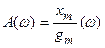и .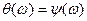

Таким образом, амплитуднаячастотнаяхарактеристикаA(w) является функцией, показывающей изменение отношения амплитуды установившихся вынужденных колебаний на выходе САУ к амплитуде гармонического воздействия на ее входе в зависимости от частоты колебаний входного воздействия.

Фазовойчастотнойхарактеристикойq(w) является функция, показывающая сдвиг по фазе между установившимися колебаниями на выходе и входе САУ при входных гармонических воздействиях в зависимости от частоты колебаний входного воздействия.

Зная амплитуду и частоту гармонического воздействия на входе САУ и ее передаточную функцию (определив по ней W(jw) и A(w), q(w)), можно аналитически определить установившееся вынужденное движение на выходе САУ:

.

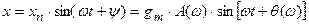На рисунке 4.7 показаны графики этих сигналов.

Частотные характеристики аналитически получаются из передаточной функции, а значит, как и она, определяют динамические свойства устройства.

В частотном методе анализа широко используется графическое представление W(jw), A(w) и q(w). Построение кривых этих функций можно произвести, вычислив, значения их для различных величин w. Очевидно, такой путь построения графиков частотных характеристик является чрезвычайно трудоемким.

Значительно проще строить и в дальнейшем работать с логарифмическими частотными характеристиками.

Логарифмическая амплитудная характеристика определяется по амплитудной частотной характеристике A(w) следующим образом:

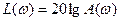
и измеряется в децибелах (дБ).

Рис. 4.7. Графики гармонических сигналов на выходе и входе САУ

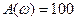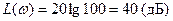Например, если , то . График L(w) строится в прямоугольной системе координат. По оси абсцисс откладываются значения w в логарифмическом масштабе, а оцифровка делений ведется в значениях w в с^-1. За единицу масштаба по оси частот (абсцисс) принимается декада.

Декадой называют отрезок на оси абсцисс (частот), соответствующий десятикратному изменению частоты. Значения L(w) в децибелах откладываются по оси ординат. Очевидно, значения L(w), соответствующие 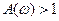, будут расположены выше оси абсцисс, L(w) для 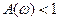– ниже ее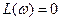, и при .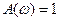

Логарифмическаяфазоваяхарактеристика j(w) отличается от обычной фазовой характеристики q(w) лишь тем, что график ее строится в прямоугольной системе координат, имеющей ту же, что и для L(w), логарифмическую ось частот. По оси ординат откладываются значения 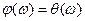в радианах или градусах.

Использование логарифмических частотных характеристик L(w) и j(w) обусловлено рядом их преимуществ по сравнению с обычными частотными характеристиками A(w) и q(w). Такими преимуществами являются: меньшая крутизна характеристики L(w), позволяющая аппроксимировать ее небольшим числом прямолинейных отрезков и облегчая ее построение; большая наглядность; возможность замены операции умножения амплитудных частотных характеристик операцией суммирования логарифмических амплитудных частотных характеристик, которая производится сравнительно просто графически и не требует вычислений. Такая возможность проявляется при определении частотных характеристик последовательно соединенных звеньев.