Понятие безрискового актива и его использование

Безрисковые активы характеризуются тем, что риск неполучения дохода от вложения в них для инвестора отсутствует. К безрисковым активам относят кредиты и облигации. При инвестировании средств в безрисковые активы строго устанавливаются: доходность (по фиксированная или плавающей ставке), порядок и сроки уплаты доходов, срок предоставления финансовых ресурсов вкладчика, порядок и сроки уплаты суммы инвестиций.

Capital Assets Pricing Model (CAPM) - модель оценки доходности финансовых активов[8]. Шарп за эту модель получил Нобелевскую премию. Эта модель устанавливает взаимосвязь между риском, доходностью рынка и доходностью безрисковых финансовых активов[9]. Теория оценки активов является продолжением теории эффективного портфеля. Точнее, распространением этой теории на включение в эффективный портфель безрискового актива. Даже удивительно, как много появляется новых следствий после столь нехитрой процедуры. Дополним портфель рискованных активов (с индексом A) безрисковым активом (с индексом rf - risk- free), у которого по определению стандартное отклонение доходности нулевое (σ_rf = 0). Очевидно, ковариация безрискового актива с любым рискованным активом равна нулю, так же, как и коэффициент корреляции. Тогда

R_Port = W_rfR_rf + W_AR_A = W_AR_A + (1 - W_A) R_rf = R_rf + W_A (R_A – R_rf)

σ²_Port = W²_A σ²_A + (1 – W_A)² σ²_rf + 2 W_A (1 - W_A) r_A,rf σ_A σ_rf = W²_A σ²_A

σ_Port = W_Aσ_A

Таким образом, и риск, и доходность объединенного портфеля линейно зависят от соответствующих величин для рискованного портфеля. Поэтому на плоскости "доходность – риск" зависимость доходности объединенного портфеля от риска выглядит как прямая линия, соединяющая безрисковый актив с любым из рискованных портфелей, лежащих на эффективной границе (рис. 1, прямая R_rfA). Для того, чтобы увеличить доходность (а заодно и риск) объединенного портфеля, нужно увеличивать долю рискованного портфеля по отношению к доле безрискового актива.

Выражение, определяющее доходность портфеля, можно переписать в виде

R_Port = R_rf + W_A (R_A – R_rf) = R_rf + [(R_A – R_rf) / σ_A] σ_Port

Здесь явно видна линейная зависимость между доходностью портфеля и стандартным отклонением его доходности. Тангенс угла наклона этой линии (R_A – R_rf) / σ_A известен как коэффициент Шарпа.

Сдвиг точки А вдоль эффективной границы вверх-вправо увеличивает эффективность объединенного портфеля (максимизирует коэффициент Шарпа) – для тех же рисков доходность становится все выше и выше. Однако всему есть предел – максимальная эффективность достигается тогда, когда прямая, соответствующая объединенному портфелю, касается эффективной границы. Точку касания принято обозначать через М (market).

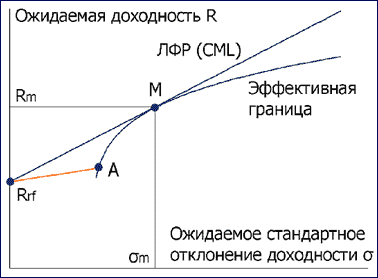
Рис. 7 Линия рынка капитала (CML)

Очевидно, с учетом безрискового актива новой эффективной границей становится прямая R_rfM (рис. 1), лежащая выше старой эффективной границы (для портфелей рискованных активов) везде, за исключением точки касания М. Эта прямая именуется линией рынка капитала, сокращенно ЛРК (CML – capital market line). Все инвесторы будут выбирать портфели именно на этой прямой, в соответствии с индивидуальной функцией полезности (в точке касания функции полезности и ЛРК). Портфели для разных инвесторов (с разным риском) будут при этом отличаться только долей безрискового актива.

Таким образом, все инвесторы будут покупать (в разных долях) один и тот же рискованный портфель, соответствующий точке М на эффективной границе. Поэтому портфель М должен включать все рискованные активы – ведь если актив не включен в такой портфель, это означает, что на него нет никакого спроса, следовательно, стоимость его нулевая. Поскольку предполагается, что рынок находится в равновесии, то необходимо, чтобы все рискованные активы были включены в портфель М в долях, пропорциональных их рыночной капитализации (для акций – произведение рыночной цены акции на количество акций в обращении). Если, например, доля актива в портфеле будет выше, чем доля в капитализации, избыточный спрос на такой актив приведет к росту его цены (и росту капитализации).

Можно добавить, что систематический (недиверсифицируемый) риск рыночного портфеля часто именуют рыночным риском. А хорошей аппроксимацией рыночного портфеля, как это следует из определения, является рыночный индекс, взвешенный по капитализации. Для рынка акций США инвесторы ориентируются на индекс S&P 500, России – индекс РТС.

А как быть, если инвестор желает взять риска больше, чем его имеется в точке М (σ_m)? В этом случае ему следует вложить в рискованный портфель М денег больше, чем у него есть, т.е. взять кредит под процент, равный R_rf. При этом доходность и риск портфеля выражаются теми же формулами, что и прежде, только W_rf становится отрицательной. И доходность, и ее стандартное отклонение продолжают оставаться линейными функциями соответствующих величин для рыночного портфеля, поэтому линия рынка капитала просто продолжается вправо-вверх. Взятию кредита соответствует смещение по этой линии правее точки М. Правда, сколь угодно далеко сместиться не удастся – регуляторы рынка (SEC в США и ФКЦБ в России) ограничивают размер кредита, который можно взять у брокера под залог уже имеющегося портфеля (маржинальное кредитование).[10]

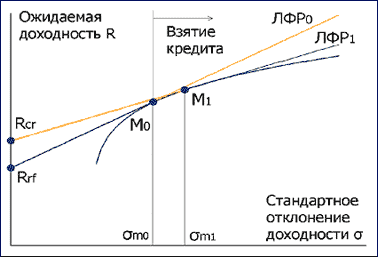
Рис. 8 Линия рынка капитала при отличии ставки кредитования от безрисковой

В реальной жизни, разумеется, ставка кредитования выше безрисковой (часто намного выше), и ЛРК становится ломаной линией (рис. 2) – она состоит из отрезков ЛРК₀ и ЛРК₁. ЛРК₁ строится исходя из точки R_cr (ставка кредитования) и касается эффективной границы не в "старой" точке М₀, а правее и выше, в точке М₁. Точка М "раздваивается" – для инвесторов, использующих кредитные средства, рыночный портфель должен быть несколько более рискованным, но обычно различиями пренебрегают.

Список использованной литературы

1. Ушакова Н.В. Методические указания по выполнению контрольно-курсовой работы по курсу: «Теоретические основы финансового менеджмента»– Тула, ТулГУ, 2006. – 29 с.

2. Владимир Детинич. В помощь инвестору. http://www.parusinvestora.ru/carticles/cart2_5.sht

3. Олег Лытнев. Курс лекций "Основы финансового менеджмента" http://www.cfin.ru/finanalysis/lytnev/5-6.shtml