Эффективная граница и случайные портфели

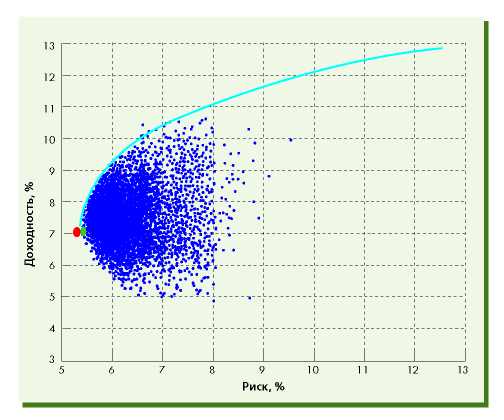
Как видно из рисунка, множество всех возможных портфелей имеет чёткую границу слева. Это значит, например, что при риске 6% из данных акций нельзя составить портфель с ожидаемой доходностью меньше 5% и больше 9%. С практической точки зрения интерес представляет верхняя часть границы, которая называется эффективной границей.

При заданном уровне риска портфеля с большей ожидаемой доходностью, чем тот, что находится на эффективной границе, не существует. И наоборот, при заданном уровне ожидаемой доходности невозможно сформировать портфель с меньшем уровнем риска.

Кроме того, существует портфель с минимально возможным риском – так называемый минимальный портфель. Портфель с меньшим риском (при любой ожидаемой доходности), чем у минимального портфеля, сформировать невозможно.

После того, как построена эффективная граница, вам осталось только выбрать на ней точку, отражающую ваши предпочтения по требуемой доходности и приемлемому риску. А мы скажем, какой портфель ей соответствует, то есть, сколько и каких акций покупать.

С момента создания классической теории появился ряд полезных усовершенствований. В частности, подобным образом можно формировать портфели с возможностью коротких продаж. Программа определит, сколько и каких акций нужно продать и как распределить средства между оставшимися. Есть и другие, более тонкие, новшества. Они связаны со способом расчёта необходимых для работы параметров – ожидаемой доходности компаний и матрицей ковариаций, отражающей степень их взаимосвязи.

Граница эффективности Гарри Макровица ясно отражена на графике ниже.

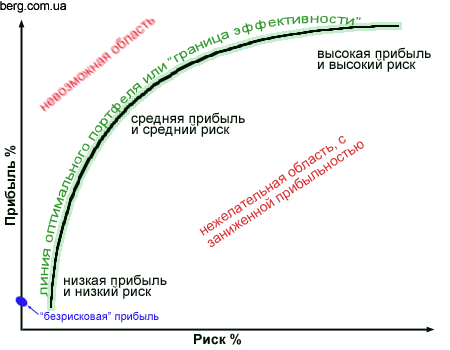
Исходя из выпуклой природы границы эффективности, становится очевидно, что наиболее выгодное соотношение прибыли к риску находится посередине. Это происходит потому, что при больших возвратах (т.е. прибыли), каждое увеличение возврата сопровождается более быстрому увеличению степени риска. Но с другой стороны, если обратить внимание на менее рисковую область, то становится понятно, что лучше вложить в т.н. “безрисковые” ЦБ (государственные и муниципальные облигации), чем нести риск из-за такой же прибыли.

Итого, график оптимального портфеля и граница эффективности демонстрируют, что:

· высокая прибыль сопровождается более высоким риском

· низкая прибыль не должна облагаться риском

Прикладной смысл модели оптимального портфеля очень прост и в то же время полезен: зная вашу ожидаемую норму доходности, вы можете вычислить справедливый процент риска. И наоборот: зная риск, который вы готовы терпеть, вы можете вычислить справедливую норму доходности для этого риска. Но сами не пытайтесь делать эти вычисления в уме. Делать соответствующие просчеты вам помогут сотрудники финансовой компании, т.к. для этого необходимо специальное программное обеспечение.

22. Портфели из двух рискованных активов»

Рискованный актив (risky asset) обеспечивает денежный поток, который, по крайней мере, частично, носит случайный характер. Цена акции изменяется ежедневно, и каждый раз, когда это происходит, собственник выигрывает или несет убытки. Другими словами, денежный поток заранее не известен доподлинно.

В общем виде формирование инвестиционного портфеля заключается в распределении инвестиций конкретным человеком. Это процесс поиска наилучшего соотношения между риском и ожидаемым уровнем доходности инвестиций с целью составления портфеля, инвестиции которого обеспечивали бы инвестору максимальную ожидаемую ставку доходности при той степени риска, на которую он согласен.

Рассмотрим портфель, состоящий из двух рискованных активов, т.е. когда у двух активов разные доходности и разные стандартные отклонения доходностей.

Формула для вычисления среднего значения ставки доходности портфеля, состоящего из двух рискованных активов имеет следующий вид:

R_Port = W₁R₁ + W₂R₂ (1)

где W₁ - это доля рискованного актива 1;

W₂ - это доля рискованного актива 2;

R₁, R₂ это доходность активов 1 и 2 соответственно.

В свою очередь формула дисперсии такова:

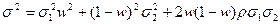(2)

σ_Port² = W₁² σ₁² + W₂² σ₂² + 2W₁W₂ r₁₂σ₁σ₂

где r_ik - коэффициент корреляции;

σ₁σ₂ – дисперсии активов.

Зависимость стандартного отклонения доходности такого портфеля от коэффициента корреляции и соотношения весов показана на рис. 6 (он построен для случая, когда и доходность, и дисперсия второго актива вдвое выше, чем у первого). На плоскости "доходность – риск" образуются эллипсы, каждому коэффициенту корреляции соответствует свой эллипс, точки на каждом эллипсе соответствуют разным соотношениям весов компонента. При полной корреляции, как положительной, так и отрицательной (r₁₂ = ±1), эллипсы вырождаются в отрезки прямых линий.

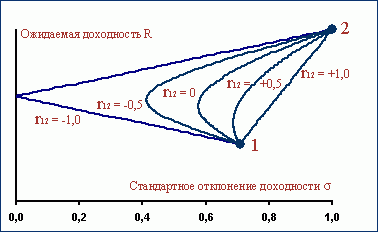
Рис. 4.5. Зависимость доходности портфеля из двух активов от коэффициента корреляции и соотношения весов (доходность и дисперсия второго актива вдвое выше, чем у первого).

На графике видно, что не только для отрицательных, но и для низких положительных корреляций существуют портфели, риск которых меньше, чем риск каждого из входящих в них активов. В самом деле, в нашем примере уже для r₁₂ = +0,5 при некоторых соотношений весов стандартное отклонение портфеля меньше, чем стандартное отклонение любого из активов. Добавляя к активу 1 некоторую долю актива 2 (с большей доходностью и более высоким риском) можно одновременно увеличить доходность портфеля и снизить его риск.

Таким образом, характерное отличие портфеля, состоящего из двух рискованных активов в том, что ожидаемая ставка доходности инвестора непредсказуема, так как у активов разные значения доходности и риска.