Нелинейная регрессия
1) Парабола 2-го порядка 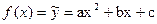 .
.
Для определения параметров a,b,c можно воспользоваться МНК.
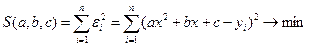
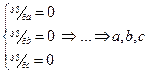
2) Гипербола 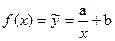 .
.
С помощью замены переменной преобразуем эту формулу к линейному виду.
Замена: X=1/x;
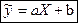
Для нахождения параметров a и b можно воспользоваться формулами:
a=Da/D, b=Db/D, заменив xi ->Xi.
| i | 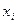
| 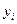
| 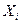
| 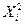
| 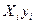
| 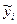
| 
|
| … n | 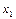
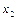 …
…
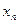
| 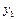
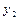 …
…
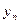
| 1/ 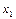 1/
1/ 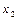 …
1/
…
1/ 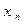
| ||||
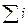
| 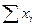
| 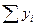
| 
| 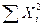
| 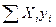
| - | 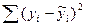
|
3) Показательная функция или экспонента (e=2,718281828459045…)
y=eax+b=(ea)xeb=AxB {A=ea, B=eb} => y=axb
ln y= ln (axb)= ln ax+ln b=x ln a+ ln b.
ln y= x ln a+ ln b
Замена: Y=ln y, A=ln a, B=ln b => a=eA, b=eB.
Y=Ax+B, A=DA/D, B=DB/D, yi -> Yi=ln yi.
Для нелинейных форм регрессии в качестве характеристики силы связи между факторным и результативным признаком следует использовать корреляционное отношение (а не коэффициент прямолинейной корреляции Пирсона!).
Общая дисперсия результирующего признака:
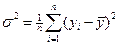 . Отражает общую вариацию результирующего признака у в зависимости от всех факторов.
. Отражает общую вариацию результирующего признака у в зависимости от всех факторов.
Факторная дисперсия (аналог межгрупповой дисперсии):
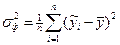 . Характеризует влияние факторного признака х на вариацию у.
. Характеризует влияние факторного признака х на вариацию у.
Остаточная дисперсия:
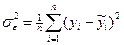 . Объясняет вариацию у от всех прочих (кроме х) факторов (аналог средней из внутригрупповых дисперсий).
. Объясняет вариацию у от всех прочих (кроме х) факторов (аналог средней из внутригрупповых дисперсий).
На основании правила сложения дисперсий, получим: s2=sф2+se2.
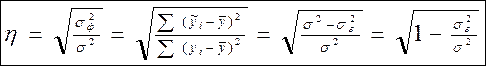
Лучшей является регрессионная модель с наибольшим значением корреляционного отношения.
Дата добавления: 2015-12-11; просмотров: 692;
