ЛЕКЦИЯ 10. Нелинейная пространственная фильтрация

В результате применения линейных сглаживающих фильтров происходит подавление шумов, но одновременно размываются границы между областями с разной амплитудой сигнала. Для уменьшения «смаза» границ разработаны различные нелинейные фильтры. Как и линейные КИХ фильтры, нелинейные фильтры работают в скользящем окне. Но, при линейной фильтрации вычисляется линейная комбинация отсчетов сигнала, а при нелинейной фильтрации выполняются нелинейные преобразования отсчетов сигнала в определяемой маской фильтра окрестности элементов.

Сигма-фильтр

Сигма-фильтр предназначен для подавления шумов в изображении с сохранением контуров (резких границ областей). Центральный элемент маски замещается взвешенным средним значением, вычисленным только по тем амплитудам отсчетов, значения которых попадают в ± kσ – область относительно яркости центрального элемента. σ выбирается либо как СКО подавляемого шума, либо как СКО в маске, либо устанавливается равной СКО, полученному по всему изображению:

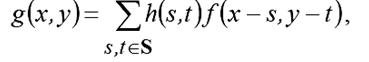
где S-окрестность составляют те значения координат маски, в которых выполняется наложенное условие:

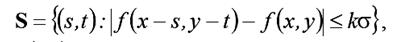
h(s,t) – КИХ линейного сглаживающего фильтра. При k = 2 диапазон заменяемых значений составляет ±2σ, в случае нормального распределения шума вероятность попадания амплитуды за пределы диапазона равна 4,55%. Фильтры, основанные на порядковых статистиках, также относятся к нелинейным фильтрам. Наиболее эффективными по совокупности воздействий: сглаживания шума на однородных участках изображения, сохранения скачков изменения яркости, минимального искажения формы

границы, подавления импульсного шума, вычислительной эффективности является медианный фильтр.

Медианный фильтр

Медианный фильтр (МФ) (предложен Тьюки в 1974 г.) заменяет центральный элемент маски медианой упорядоченной (по невозрастанию или по неубыванию амплитуды) выборки, сформированной из всех амплитуд отсчетов, покрываемых маской фильтра. При применении МФ происходит последовательная обработка каждой точки кадра, в результате чего образуется последовательность оценок. При медианной фильтрации используется скользящее двумерное окно. В принципе, для каждого отсчета выполняется независимая оценка медианы в окне. В целях ускорения оценки целесообразно алгоритмически на каждом шаге использовать ранее выполненные вычисления. Размер окна устанавливается нечетным и равным m× n . Отсчеты изображения, оказавшиеся в пределах окна, образуют рабочую выборку текущего отсчета. Если упорядочить последовательность {fi , i = [1, mn]} по неубыванию, то ее медианой будет тот элемент выборки, который занимает центральное положение в этой упорядоченной последовательности. Этот элемент является (mn + 1)/ 2 наибольшим и (mn + 1)/ 2 наименьшим значением в выборке и определяет результат медианной фильтрации для текущей точки кадра. Введем формальное обозначение описанной процедуры в виде:

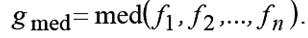
Рассмотрим пример. Предположим, что упорядоченная последовательность Yв окне размером 3x3 имеет вид: Y={99,140,97,150,255,155,158,99,175}, где элемент 255 соответствует центру окна (x, y). Большое значение яркости в этой точке кадра является результатом воздействия импульсной помехи. Упорядоченная по неубыванию выборка имеет вид: {97,99,99,140,150,155,158,175,255}, следовательно, в соответствии с процедурой, на выходе медианного фильтра получаем gmed =150. Видим, что учет яркостей элементов окрестности при фильтрации в текущей точке привел к подавлению импульсной помехи. Если импульсная помеха не является точечной, а занимает некоторую область, то она также может быть подавлена, если размер этой локальной области будет меньше, чем половина размера апертуры МФ. Поэтому для подавления импульсных помех, поражающих локальные участки изображения, следует увеличивать размеры апертуры МФ.

Действие МФ состоит в “игнорировании” как положительных, так и отрицательных выбросов значений входной выборки. Такой принцип подавления помехи может быть применен и для ослабления шума на изображении. Однако исследование подавления шума при помощи медианной фильтрации показывает, что ее эффективность при решении этой задачи ниже, чем у линейной фильтрации. Медианная фильтрация лучше сохраняет границы изображения, чем любая линейная фильтрация. Механизм этого явления очень прост и заключается в следующем. Предположим, что окно фильтра находится вблизи границы, разделяющей светлый и темный участки изображения, при этом его центр располагается в области темного участка. Тогда рабочая выборка будет содержать большее количество элементов с малыми значениями яркости, следовательно, и медиана будет находиться среди элементов с малыми значениями яркости. И наоборот, если центр окна смещен в область более высокой яркости, то и медиана будет находиться в области более высокой яркости. Это позволяет при применении МФ сохранить перепады яркости.

Медианные фильтры подавляют импульсные шумы. К таким шумам относится и шум типа «соль и перец», отсчеты которого имеют значения, соответствующие максимальному («соль») и минимальному («перец») уровням квантования в сигнале изображения. Резкие изменения амплитуды сохраняются медианным фильтром, а импульсная помеха, размер которой ≤ mn / 2 , таким фильтром подавляется. Однако при увеличении маски фильтра можно потерять информацию о малоразмерных областях изображения и произвести искажение границ областей, особенно в угловых положениях.

На рисунке 10.1 приведен синтезированный пример, иллюстрирующий исчезновение линии толщиной 1 элемент на изображении, полученном после применения медианного фильтра размером 3×3.

а) б) в)

Рисунок 10.1 – Применение медианного фильтра с окном 3×3 элемента: а) исходное изображение; б) результат работы фильтра; в) разностное изображение

Несмотря на подавление сигнала и в некоторых других областях (черные точки на разностном изображении рисунке 10.1 в) границы областей не размыты. Цифровое цветное изображение, представленное в RGB цветовом координатном пространстве, является трехкомпонентным двумерным сигналом. Каждый элемент цифрового растрового цветного изображения размера MxN может быть представлен вектором:

C(x,y)=[R(x,y),G(x,y),B(x,y)],

где x – номер столбца, y – номер строки, x ∈[0,N −1], y ∈[0,M −1]. R(x,y), G(x,y), B(x,y)- R, G, B-компоненты элемента с координатами растра (x,y).

При создании векторных медианных фильтров вводят меру расстояния между векторами. Функция расстояния между двумя векторами Ci и Cj в пространстве RGB в общем виде задается формулой:

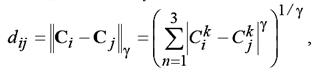
где k – номер компонента вектора, γ – характеристика метрики.

В случае евклидова расстояния (метрика L² , γ =2)

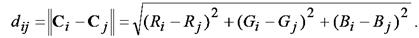
Множество входных векторов в скользящем окне фильтрации обозначим

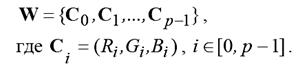
Расстояние для j-го вектора оценивается как сумма расстояний от j-го вектора до каждого из векторов в окне:

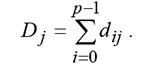
Последовательность расстояний {D0 ,D1,...,Dp−1} упорядочивают по возрастанию, и в качестве отклика фильтра используют вектор C_i, соответствующий минимальному расстоянию D_i = min {D_j}. Другие медианные векторные фильтры отличаются мерой расстояний и весовыми функциями, используемыми для взвешивания суммы.

Другой подход основан на каскадной схеме многоканальной фильтрации, которая позволяет подавить импульсную помеху и в большей степени сохранить границы объектов, поскольку МФ выполняется в направлении границы и в минимально возможном окне.

Поскольку применение МФ приводит все же к подавлению ВЧ изображения, вызывая размывание краев и текстур, в настоящее время получают все большее развитие схемы адаптивной фильтрации, которые позволяют изменить импульсную характеристику фильтра в зависимости от локального значения сигнала изображения.