ЛЕКЦИЯ 12. Дифференциальные методы выделения контуров
Одним из наиболее очевидных и простых способов обнаружения границ является дифференцирование яркости, рассматриваемой как функция пространственных координат. То, что дифференцирование дает желаемый эффект, видно из простого «одномерного» примера. До дифференцирования сигнал имеет вид, представленный на рисунке 12.1а. После дифференцирования – вид на рисунке 12.1б, и теперь контур легко выделяется пороговой обработкой (рисунок 12.1б).
Очевидно, в двумерном случае, если мы имеем изображение со значениями яркости f(x1, x2), то обнаружение контуров, перпендикулярных оси x1, обеспечивает взятие частной производной ¶f/¶x1, а перпендикулярных оси x2 – частной производной ¶f/¶x2 (рисунок 12.2). Эти производные характеризуют скорости изменения яркости в направлениях x1 и x2 соответственно.
 Можно вычислить производную и по произвольному направлению. Нам однако необходимо найти характеристику, позволяющую обнаружить контур независимо от его ориентации. В качестве такой характеристики, являющейся признаком наличия контура в локальной области, можно использовать градиент яркости:
Можно вычислить производную и по произвольному направлению. Нам однако необходимо найти характеристику, позволяющую обнаружить контур независимо от его ориентации. В качестве такой характеристики, являющейся признаком наличия контура в локальной области, можно использовать градиент яркости:
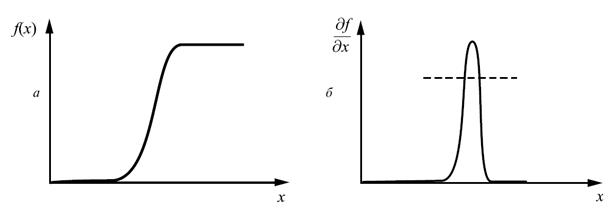
Рисунок 12.1 – Дифференциальный метод выделения контура
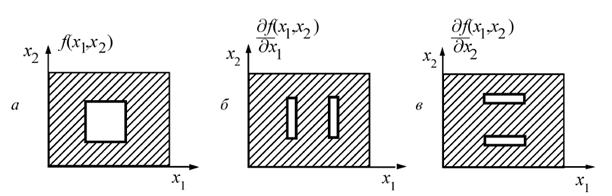
Рисунок 12.2 – Дифференциальный метод выделения контура на изображении
Градиент — это вектор (в нашем случае в двумерном пространстве), ориентированный по направлению наиболее быстрого возрастания функции f(x1, x2) и имеющий длину, пропорциональную этой максимальной скорости (максимальному значению частной производной по направлению) (рисунок 12.3). Так как направление нас не интересует, ограничимся рассмотрением модуля градиента (длины вектора):
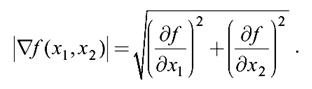
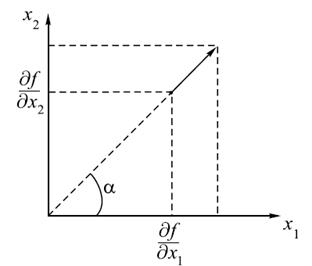
Рисунок 12.3 – К определению градиента функции
Отметим, что для вычисления модуля градиента вместо производных ¶f/¶x1 и ¶f/¶x2 можно брать производные по любой паре перпендикулярных направлений. Итак, для выделения контура произвольного направления можно использовать модуль градиента поля яркости.
В случае цифровых изображений, представленных матрицей отсчетов, вместо производных берутся дискретные разности:
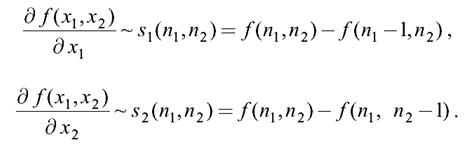
Тогда преобразование, выделяющее перепады яркости, будет заключаться в вычислении модуля «дискретного градиента изображения» f(n1, n2):
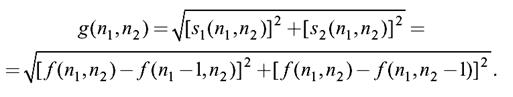
Видно, что это вычисление производится в два этапа. Сначала изображение обрабатывается двумя двумерными КИХ-фильтрами для получения дискретных разностей. Импульсные характеристики этих систем соответствуют «маскам» размерами 2×1 и 1×2:
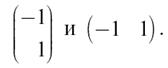
На втором шаге вычисленные разности нелинейным образом комбинируются для получения g(n1, n2). При реализации процедуры детектирования контуров стараются избегать трудоемких операций типа умножения и извлечения квадратного корня. Поэтому используют выражения, вычисляемые проще, «аппроксимирующие» дискретный градиент. Чаще всего модуль градиента заменяют выражениями
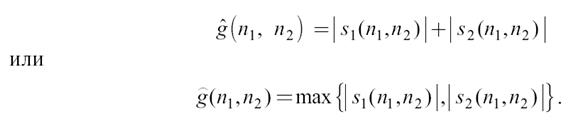
Следует заметить, что такие приближения градиента уже не являются одинаково чувствительными к границам с любой ориентацией. Действительно, для строго вертикальных или горизонтальных границ все три формулы дают одинаковые результаты. Но для границы с наклоном 45°, при котором s1(n1, n2) = s2(n1, n2), имеем:
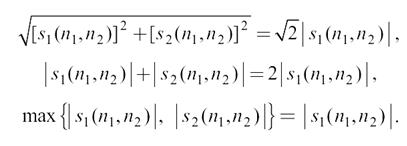
Приближенные значения градиента отличаются от точного в 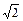 раз. Однако такие вариации на практике считаются приемлемыми.
раз. Однако такие вариации на практике считаются приемлемыми.
Дата добавления: 2015-12-16; просмотров: 1826;
