ЛЕКЦИЯ 14. Методы выделения перепадов яркости с согласованием
Общим недостатком рассмотренных выше методов выделения перепадов яркости является высокая чувствительность к шуму. Это объясняется тем, что действие разностных операторов состоит в вычислении и комбинировании разностей отсчетов в пределах «окна» малых размеров. Каждая разность вычисляется непосредственно по отсчетам, поэтому шум на изображении попадает в результат преобразования с усилением.
В то же время сам подход к выделению контуров с помощью локальных преобразований изображения скользящим окном представляется довольно естественным и очень удобным для реализации. Можно, сохранив достоинство дифференциальных методов, повысить их помехоустойчивость, если перед применением дифференциального оператора применить сглаживание значений яркости в пределах окна, то есть согласовать с ними некоторую поверхность первого или второго порядка. Такой подход реализуется дифференциальными методами с согласованием.
Рассмотрим метод согласования на примере обработки изображения окном 2×2. Учтем, что дискретное изображение получено из непрерывного:
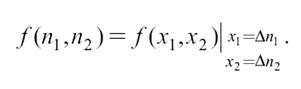
По наблюдаемым значениям яркости в пределах выбранного «окна»
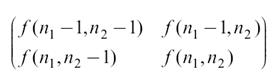
построим на нем аппроксимирующую плоскость:
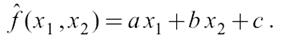
Если плоскость построена, то есть определены коэффициенты a, b, и c, а значит известны частные производные
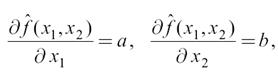
то можно вычислить искомый модуль градиента, который служит признаком локального перепада яркости:
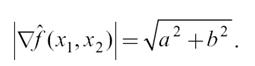
При построении плоскости удобнее всего воспользоваться методом наименьших квадратов. При поиске коэффициентов будем минимизировать величину
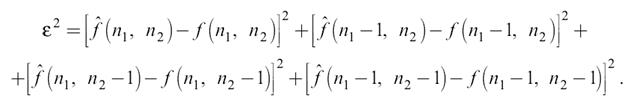
Для любого положения окна коэффициенты будут определятся одинаковыми функциями отсчетов, поэтому возьмем окно при n1 = n2 = 1, для которого все выкладки будут более компактными. Итак, на рассматриваемом окне
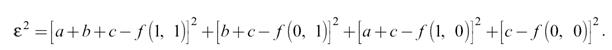
В точке минимума все производные погрешности аппроксимации по коэффициентам равны нулю:
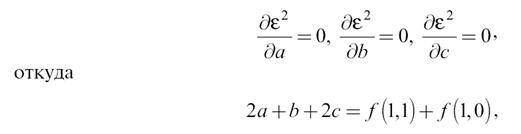
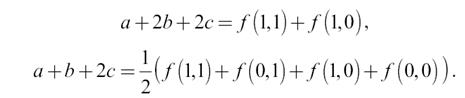
Окончательно выражения для коэффициентов будет иметь вид
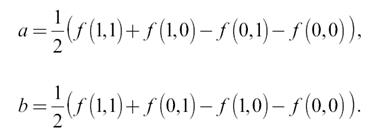
Коэффициенты a, b могут быть вычислены путем линейной обработки изображения масками 2×2, что равнозначно усреднению дискретных разностей по окну 2×2. При этом градиент менее чувствителен к шуму.
Теперь сделаем очевидное обобщение. В общем случае построение процедуры, использующей дифференциальный метод с согласованием, заключается в следующем. Вокруг обрабатываемой точки на изображении задается некоторая область — «окно обработки». По отсчетом окна строится аппроксимирующая полиномиальная поверхность. Естественно, нужно выбирать такой порядок поверхности, чтобы число коэффициентов было меньше числа пикселей в окне. Для получения изображения с подчеркнутыми перепадами вычисляется дифференциальная характеристика (градиент или лапласиан) аппроксимирующей поверхности в центре окна.
Дата добавления: 2015-12-16; просмотров: 1711;
