Измерение тесноты связи признаков шкалы наименований.
А) Связь 2-х альтернативных признаков (измеримых по шкале дихотомии)
X:{0,1}
Y:{0,1}
В этом случае строится таблица сопряженности 2х2:
| Y \ X | S | ||
| a | b | a+b | |
| c | d | c+d | |
| S | a+c | b+d | N |
Здесь, например, параметр b - число элементов выборки, имеющих значение 0 признака Y и 1 - признака X.
Для анализа тесноты связи в данном случае можно использовать коэффициент ассоциации Пирсона:
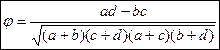
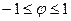
Или коэффициент контингенции Юла:
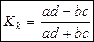
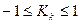
Пример: Оценить связь между предпочтением при голосовании на выборах избирателей (Y) и фактом наличия у избирателей работы (X).
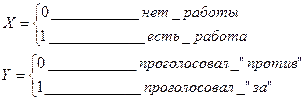
Обследованию подверглись 200 человек.
| Y X | S | ||
| S |
Требуется вычислить j и Kk
Б) Признаки, измеренные по шкале наименований с числом значений больше двух.
| X Y | … | nx | S | ||
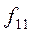
| 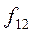
| … | 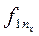
| 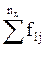
| |
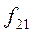
| 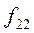
| … | 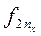
| 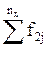
| |
| … | … | … | … | … | … |
| ny | 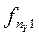
| 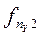
| … | 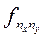
| 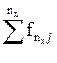
|
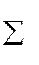
| 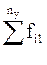
| 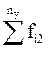
| … | 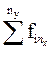
| 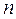
|
nx – число возможных значений признака X.
ny– число возможных значений признака Y.
Используется коэффициент взаимной сопряженности Чупрова:
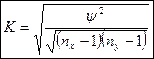
Используется также коэффициент сопряженности Пирсона:
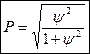
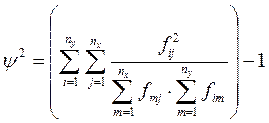
Здесь в знаменателе 1-го слагаемого стоит произведение сумм элементов строки i и столбца j, на пересечении которых стоит частота fij.
Дата добавления: 2015-12-11; просмотров: 866;
