Целью регрессионного анализа в случае парной регрессии является предсказание значения результативного признака Y при определенном значении факторного признака X
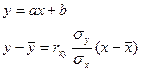
В случае множественной корреляции исследуется зависимость отклика системы от нескольких факторов
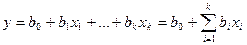
Изучение множественной корреляции начинается с анализа матрицы парных коэффициентов корреляции, что позволяет произвести отбор факторов, включаемых в модель множественной зависимости
| Признак | y | x1 | x2 | … | xk |
| y | ry,x1 | ry,x2 | … | ry,xk | |
| x1 | rx1,y | rx1,x2 | … | rx1,xk | |
| x2 | rx2,y | rx2,x1 | … | rx2,xk | |
| … | … | … | … | … | … |
| xk | rxk,y | rxk,x1 | rxk,x2 | … |
При построении многофакторных моделей должно соблюдаться требование наименьшей коррелируемости включенных в модель признаков–факторов, т.е. отсутствия мультиколлинеарности.  . При невыполнении хотя бы одного неравенства следует исключить факторный признак с менее тесной связью с Y.
. При невыполнении хотя бы одного неравенства следует исключить факторный признак с менее тесной связью с Y.
Следует учитывать, что число факторов, включаемых в модель, должно быть в 5-6 раз меньше, чем число единиц, входящих в совокупность.
Совокупный коэффициент корреляции определяется следующим образом:
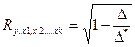
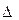 - определитель матрицы парных коэффициентов корреляции,
- определитель матрицы парных коэффициентов корреляции,
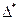 - определитель матрицы, получаемый из матрицы парных коэффициентов корреляции путем вычеркивания 1 строки и 1 столбца,
- определитель матрицы, получаемый из матрицы парных коэффициентов корреляции путем вычеркивания 1 строки и 1 столбца,
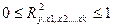 - коэффициент детерминации. Он показывает, в какой мере вариация результативного признака обусловлена влиянием признаков-факторов, включенных в уравнение множественной регрессии. R не может быть меньше, чем любой из образующих его парных коэффициентов корреляции. Чем ближе R к 1, тем меньше роль неучтенных в модели факторов и тем более оснований считать, что параметры регрессионной модели верно отражают степень эффективности включенных в нее факторов.
- коэффициент детерминации. Он показывает, в какой мере вариация результативного признака обусловлена влиянием признаков-факторов, включенных в уравнение множественной регрессии. R не может быть меньше, чем любой из образующих его парных коэффициентов корреляции. Чем ближе R к 1, тем меньше роль неучтенных в модели факторов и тем более оснований считать, что параметры регрессионной модели верно отражают степень эффективности включенных в нее факторов.
Для сравнения роли различных факторов в формировании моделируемого показателя определяют α-коэффициенты (коэффициенты эластичности) и β-коэффициенты.
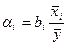 показывает, на сколько процентов в среднем изменяется результативный признак Y c изменением фактора Xi на 1%. bi – коэффициент регрессии при i-ом факторе.
показывает, на сколько процентов в среднем изменяется результативный признак Y c изменением фактора Xi на 1%. bi – коэффициент регрессии при i-ом факторе.
β-коэффициент показывает, на какую часть среднего квадратического отклонения изменится результативный признак при изменении соответствующего фактора Хi на величину его среднего квадратического отклонения:
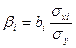
Рассмотрим простейшую модель линейной регрессии с 2-мя факторами X и Z
Y=b0+b1x+b2z
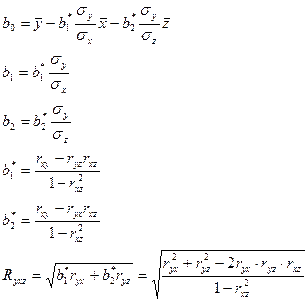
Частная корреляция
Если имеются 3 признака XYZ и известны коэффициенты корреляции между ними, то можно определить частные коэффициенты корреляции, которые показывают тесноту корреляционной связи между двумя из этих величин, при условии, что третья величина постоянная, т.е. влияние этой величины на корреляцию между двумя другими исключено.
Пример: Частный коэффициент корреляции между двумя коэффициентами Y и X при постоянном признаке Z:
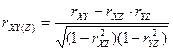
Временные ряды
Временной (динамический ряд) – последовательность значений некоторого статистического показателя в определенные интервалы (или моменты) времени.
Значения показателя – уровни ряда.
Уровни динамического ряда могут быть абсолютными, средними или относительными величинами.
Временные ряды делятся на интервальные и моментные.
В интервальном ряду приводятся данные, характеризующие величину показателя за определенный период.
Пример: Объем продаж телевизоров LG в магазине Элекам по месяцам:
| ti | yi | y`i |
В моментном ряду динамики приводятся данные характеризующие явления на определенные моменты времени или дату. Уровни моментных динамических рядов суммировать нельзя.
Пример моментного ряда – величина суммы вклада на 1 число каждого месяца.
При формировании рядов динамики следует соблюдать сопоставимость уровней, образующих ряд (одинаковая методология их исчисления), одинаковая полнота охвата различных частей явления представляемого рядом динамики.
Для моментных рядов характерна неизменность даты учета (количество товара на складе на первое число месяца)
Дата добавления: 2015-12-11; просмотров: 821;
