Способ отсчета времени от условного начала.
Используется для упрощения вычислений. Он состоит в переходе к условным моментам времени, для которых выполняется 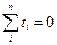 .
.
При этом 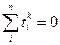 k=1,3,5,…
k=1,3,5,…
Если число уровней ряда n нечетное то момент времени посередине ряда – ноль. Все последующие моменты обозначаются с шагом (+1), предыдущие (–1). Если n - четное, то шаг=2. Посередине (-1) и (+1). Последующие (+2) предыдущие (-2)
… -2 -1 0 +1 +2 …
… -5 -3 -1 +1 +3 +5 …
Тогда система решается так:
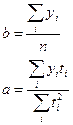
Некоторые нелинейные тренды допускают линеаризацию, например гипербола:
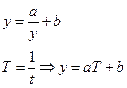
В случае гиперболы условными моментами времени пользоваться нельзя.
Линейный тренд характеризуется стабильными абсолютными цепными приростами:
t=0 y=b
t=1 y=b+a ∆=a
t=2 y=b+2a ∆=a
Показательный тренд (y=bat ) характеризуется стабильными темпами роста:
t=0 y=b
t=1 y=ba Тр=a
t=2 y=ba2 Тр=a
Преобразуем показательное уравнение:
ln(y)=ln(bat)=t*ln(b) + ln(a)
Y = At + B, где Y = ln(y), A = ln(a), B = ln(b)
Обычными методами находим A и B и делаем обратную замену.
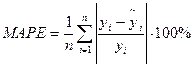 д.б. < 5-7%
д.б. < 5-7%
Анализ сезонности
1) Аддитивная модель
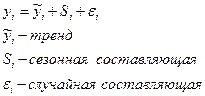
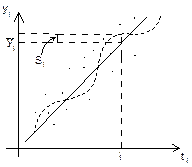
Аддитивную модель используют в случае, когда амплитуда временного ряда, имеющего тенденцию, не изменяется 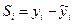
2) Мультипликативная модель
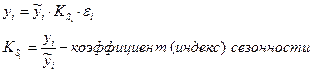

В случае стационарного ряда (отсутствие тенденции) можно использовать как аддитивную, так и мультипликативную модель.
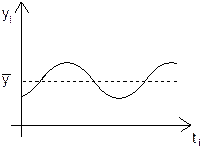
Анализ сезонных колебаний для динамического ряда, имеющего тенденцию.
В таблице приведено количество официально зарегистрированных безработных в районе (Yi , тыс. чел.).
| Квартал | 2012 г. | 2013 г. | 2014 г. | |||||||||
| Yi | Yi~ | Si | KSi | Yi | Yi~ | Si | KSi | Yi | Yi~ | Si | KSi | |
| I | - | - | - | 20.1 | 3.9 | 1.194 | 18.4 | 3.6 | 1.196 | |||
| II | - | - | - | 19.8 | -0.8 | 0.960 | 17.8 | -0.8 | 0.955 | |||
| III | 20.6 | -4.6 | 0.777 | 19.3 | -4.3 | 0.777 | - | - | - | |||
| IV | 20.4 | 1.6 | 1.078 | 18.8 | 1.2 | 1.064 | - | - | - |
Сглаживание уровней произведено с периодом в 4 квартала (1 год) с последующим центрированием уровней.
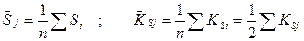
При анализе сезонности также можно использовать ряд Фурье. Для практических расчетов в нем можно ограничиться 2-3 гармониками.
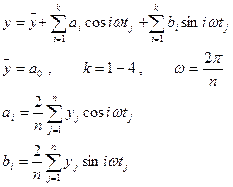
Для временного ряда, имеющего тенденцию, ряд Фурье следует применять не к исходным уровням динамического ряда yj, а к разностям yj – yj~ , где yj~ - значение, полученное в результате выравнивания исходных значений yj либо по линейному тренду yj~=atj+b, либо методом скользящей средней величины с периодом скольжения, равным году (4 квартала или 12 месяцев)
Индексы
Индекс – это показатель сравнения двух состояний одного и того же явления. Каждый индекс включает в себя данные за 2 периода:
1) отчетный (сравниваемый или текущий)
2) базисный.
Индексы, рассчитываемые по отдельным единицам, называются индивидуальными и обозначаются i. Сводный или общий индекс отражает изменения обобщенных величин по всей совокупности, обозначается I.
Индекс называется аналитическим, если изученный признак рассматривается не изолированно, а во взаимосвязи с другими признаками. Помимо обобщенной характеристики динамики непосредственных несоизмеримых явлений, аналитические индексы выполняют аналитические функции, то есть позволяет измерить вклад отдельных факторов в совокупные изменения результата.
Сводные аналитические индексы в зависимости от методов построения подразделяются на агрегатные и средневзвешенные из индивидуальных.
Пример построения индекса для следующей мультипликативной системы признаков:
q - объем продаж, p - цена, w=qp - товарооборот.
Тогда индивидуальный индекс запишется:
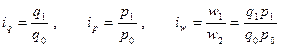
Здесь q1 – объем продаж по отдельным элементам совокупности в отчетном периоде, q0 – в базисном.
Агрегатные индексы:
| Форма индексов | Название индексов | |
| Индекс объема реализации | Индекс цен | |
| Индекс Ласпейреса | ||
| Индекс Пааше | ||
| Индекса Фишера | ||
| Индекс Эджворта-Маршалла | 
| 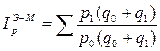
|
Сводный индекс товарооборота является простым и вычисляется по формуле: 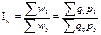 .
.
Индекс товарооборота также может быть найден через взаимосвязь индексов (мультипликативная модель):
 .
.
Рассмотрим также и разности числителей и знаменателей соответствующих индексов:
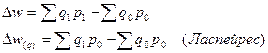
Разность числителя и знаменателя индекса физического объема в форме Ласпейреса  показывает, как в абсолютном выражении изменяется товарооборот за счет роста (сокращения) физического объема продаж.
показывает, как в абсолютном выражении изменяется товарооборот за счет роста (сокращения) физического объема продаж.
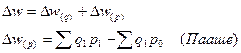
Можно записать и по-другому:
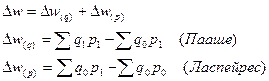
Участие каждого фактора в формировании общего изменения товарооборота в относительном выражении определяется по следующим формулам:
1. Прирост или уменьшение товарооборота за счет изменения физического объема продаж.
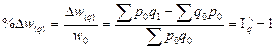
2. Прирост или снижение товарооборота за счет изменения цен:
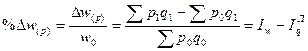
3.Совокупное влияние факторов в относительном выражении отражается следующей моделью:
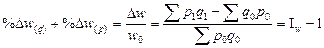
Дата добавления: 2015-12-11; просмотров: 1498;
