Коэффициент прямолинейной корреляции Пирсона (Pearson).
Используется для оценки тесноты связи между факторным и результативным признаком если:
1) Значения признаков измерены по сильной шкале (интервальной или шкале отношения).
2) Значения признаков должны подчиняться нормальному закону распределения.
3) Точки на корреляционном поле должны располагаться вдоль некоторой прямой.
Корреляционный момент (ковариация или коэффициент ковариации)
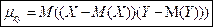
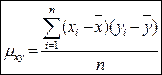
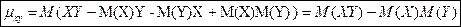
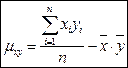
Коэффициент прямолинейной корреляции Пирсона ( Pearson ).
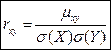
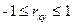
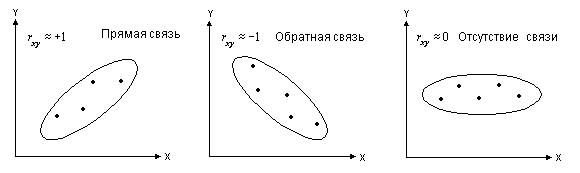
Для качественной оценки силы связи обычно используют шкалу Чеддока:
| | rxy| | 0.1-0.3 | 0.3-0.5 | 0.5-0.7 | 0.7-0.9 | 0.9-0.99 |
| Характеристика силы связи | Слабая | Умеренная | Заметная | Высокая | Весьма высокая |
При rxy=1 связь является функциональной, а при rxy<0.1 говорят об отсутствии связи.
Определение: Квадрат коэффициента прямолинейной корреляции Пирсона называется коэффициентом детерминации (индексом детерминации) 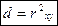 .
.
Показывает, какая доля вариации результативного признака (Y) объясняется вариацией факторного признака (X). Если rxy=0.7, то это говорит о том, что связь заметная или высокая, при этом d=0.72=0.49. То есть факторный признак x оказывает менее 50% влияния на результативный признак в числе прочих факторов. Если rxy=0, то признаки называются некоррелированными.
Независимые признаки всегда некоррелированны, так как:
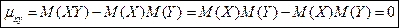
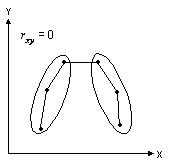
Некоррелированные же величины (rxy=0) могут быть и зависимыми
Дата добавления: 2015-12-11; просмотров: 972;
