Свойства средней арифметической.
1). 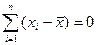
2). 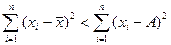 - сумма квадратов отклонений от средней арифметической меньше суммы квадратов отклонений от произвольного числа А.
- сумма квадратов отклонений от средней арифметической меньше суммы квадратов отклонений от произвольного числа А.
3). 
4). 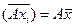 - если каждую варианту умножить или разделить на число А, то среднее увеличится в А раз.
- если каждую варианту умножить или разделить на число А, то среднее увеличится в А раз.
5). 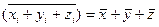
6). 
То есть, если каждый весовой коэффициент в формуле средней арифметической взвешенной умножить (разделить) на некоторое число, то средняя при этом не изменится.
Пример: Рассчитать среднюю выработку одного рабочего по следующим данным:
| Рабочий | Произведено за неделю | Часовая выработка |
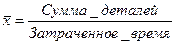
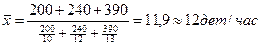
Неверный способ: (200+240+390)/3
Средняя величина является реальной величиной, поскольку она рассчитывается на основе фактически существующих данных, но вместе с тем она является абстрактной величиной, поскольку получена в результате расчетов.
Изучение вариации.
Вариация – различие значений признака у отдельных единиц изучаемой совокупности в один и тот же период или момент времени.
Статистический анализ вариации предполагает выполнение следующих основных этапов:
1.Построение вариационного ряда.
2.Графическое изображение вариационного ряда.
3.Расчет показателей центра распределения и структурных характеристик вариационного ряда.
4.Расчет показателей размера и интенсивности вариации.
5.Оценка вариационного ряда на асимметрию и эксцесс.
Построение вариационного ряда - это упорядоченное распределение единиц совокупности по возрастающим или убывающим значениям признака и подсчет числа единиц с тем или иным его значением.
Варианты – это значения, которые принимает исследуемый признак.
Частоты – это абсолютная численность отдельных групп с различными значениями признака.
Частости (относительные частоты) – это удельные веса (доли) отдельных групп в общей численности совокупности.
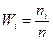 ;
; 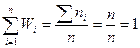 ;
;
Пример: Имеются данные о проценте выполнения сменных заданий для сотрудников фирмы. Упорядочив их по возрастанию, получим вариационный ряд.
| № | ||||||||||||||
| Фамилия | О | К | С | А | Е | Р | В | Ж | Г | Б | З | Л | М | Т |
| %, (xi) |
| Ю | Я | Н | Э | М | Д |
Объединив одинаковые значения Xi , получим таблицу, называемую рядом частот.
| xi | ||||||||||||||||
| ni |
В вариационном ряду xi получены по сильной шкале. Можно перейти в порядковую шкалу, сопоставив каждому значению ранг. Ранг равен порядковому номеру i значения xi в упорядоченной выборке, если частота ni данного значения равна 1. Если же частота значения ni >1, то ранг значения xi равен среднему арифметическому порядковых номеров этого значения в упорядоченной выборке.
| xi | i | ранг |
| 3,4,5 10,11 17,18 | 10,5 17,5 |
Дата добавления: 2015-12-11; просмотров: 605;
