Характеристики вариационного ряда.

1. Показатели центра распределения.

- Среднее значение признака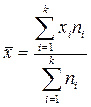

- Мода (M_o)

M_o – значение признака, наиболее часто встречающееся в изучаемой совокупности. В дискретном вариационном ряду модой является варианта с наибольшей частотой или частностью.

В интервальном вариационном ряду мода рассчитывается по формуле:

(*)

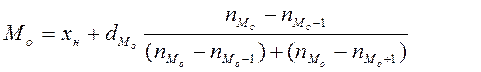Модальный интервал – это интервал, имеющий наибольшую частоту.

Расчет модального значения для вариационных рядов с неравными интервалами осуществляется по формуле аналогичной (*), только вместо показателей частот или частостей используются показатели абсолютной или относительной плотности распределения, которые обеспечивают сопоставимость неравных интервалов. Показатели плотности распределения находятся как отношения частот (частостей) к величине интервала.

- абсолютная плотность распределения

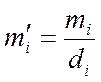- относительная плотность распределения

- Медиана (Me, Md)

Это варианта, расположенная в середине упорядоченного вариационного ряда, делящая его на две равные части так, что половина единиц совокупности имеет значение признака меньшее, чем медиана, а половина – большее, чем медиана.

Me=3

Если n=2k+1, Me=X_k+1 ;

Если n=2k, Me=(X_k+X_k+1)/2

Нормальный закон распределения

Функция плотности вероятности для нормального закона распределения:

График такой функции называется кривой Гаусса.

e=2.718281828459045…

Правило «трех сигм»:

Площадь под кривой Гаусса в диапазоне

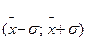составляет 68.3%

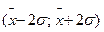составляет 95.4%

составляет 99.7%

Моменты распределения

Начальным моментом k-го порядка называется величина:

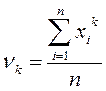
Центральным моментом k-го порядка называется величина:

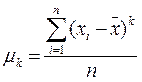
Дисперсия – это центральный момент 2-го порядка.

Средняя арифметическая – начальный момент 1-го порядка.

Основным моментом k-го порядка называется величина:

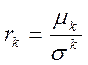(безразмерная величина)

- Асимметрия

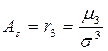µ₁=M(X-M(x))=0

-Эксцесс

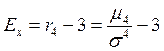
Для нормального распределения показатели асимметрии и эксцесса равны 0.

Степень существенности (или значимости) асимметрии и эксцесса можно оценить с помощью соответствующих среднеквадратических ошибок коэффициента асимметрии и эксцесса.

; ;

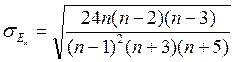Если 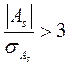- то значение A_s существенно (или значимо).

Если - то значение E_x существенно (значимо).

Для симметричного распределения .

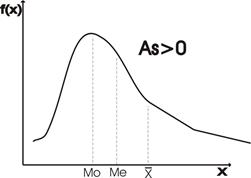
Правосторонняя асимметрия: