Определение зависимости стойкости инструмента от его параметров
Стойкость инструмента зависит от совместного действия большого числа факторов. Случайный характер их изменения обусловливает многообразие причин выхода инструмента из строя и значительные колебания в величине стойкости. Изучение эмпирических рядов стойкости инструмента показывает, что долговечность инструмента следует рассматривать как статистическую величину, представляющую собой результат действия множества факторов, влияние каждого из которых намного перекрывается суммарным влиянием всех остальных.
Среди множества факторов необходимо выделить наиболее вероятностные факторы стойкости инструмента. Для этой цели используют корреляционный анализ. Возьмем две величины x и y.
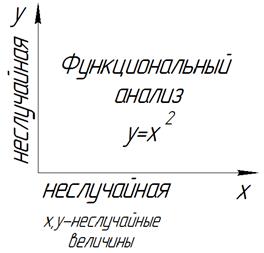
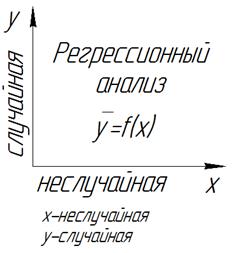
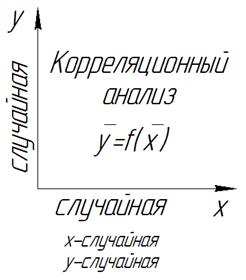
Корреляция - это статистическая связь, когда с изменением одной случайной величины х, получаем распределение вероятностей другой случайной величины y.
Корреляционный анализ заключается в поисках ответов на следующие вопросы:
1. Существует ли связь между исследуемыми параметрами?
2. Каковы форма и сила этой связи?
Статистические исследования разрушения инструмента на основе изучения рассеивания позволяют с высокой достоверностью выделить наиболее вероятные факторы стойкости и надежности инструмента. Для этой цели используют теорию корреляции, т. е. такую связь, при которой с изменением одной случайной величины получается определенное распределение вероятностей другой величины. Отыскание уравнения этой связи и является первой основной задачей теории корреляции. Второй задачей является определение тесноты корреляционной связи, т. е. степени близости ее к функциональной.
Корреляционные уравнения дают возможность вычислить вероятностные значения одной случайной величины в зависимости от отдельных значений других случайных величин. Вычисление вероятностных значений по корреляционным уравнениям имеет большую практическую ценность для тех случаев, когда непосредственное определение изучаемого признака сопряжено с порчей инструмента или со значительной трудностью испытания.
Основным способом вычисления коэффициентов корреляционных уравнений является способ наименьших квадратов. Пусть искомое корреляционное уравнение приведено к линейному виду 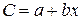 , где а и b — неизвестные параметры. Найдем прямую, которая подходила бы к заданным на границе точкам j ближе любой другой прямой:
, где а и b — неизвестные параметры. Найдем прямую, которая подходила бы к заданным на границе точкам j ближе любой другой прямой:
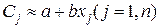 . (4)
. (4)
Коэффициенты а и b отыскивают из условия, что сумма квадратов разностей между левой и правой частями приближенного уравнения (4) обращается в минимум, т. е.
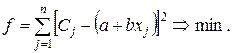
Значения а и b, удовлетворяющие минимуму функции, определяются из уравнений
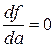 и
и 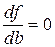 .
.
Произведя соответствующие выкладки получаем систему двух уравнений первой степени относительно неизвестных а и b:
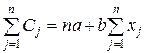 ,
,
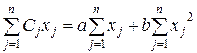
Аналогично вычисляются коэффициенты корреляционных уравнений степенного С= ахb, показательного С = abx, логарифмического
С = а + b lgx и периодического видов:
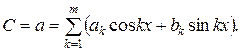
Для численного выражения степени тесноты связи между случайными величинами х = h/Н и С используется коэффициент корреляции
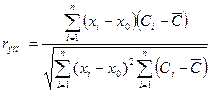 , где
, где 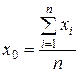
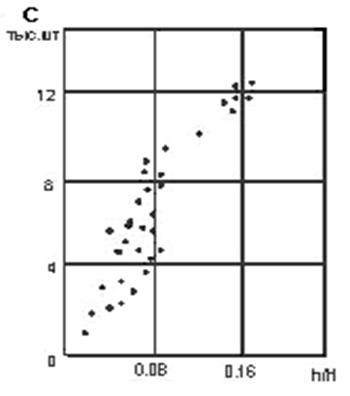
Рисунок 10 - Поле корреляции средней стойкости штампа
от отношения высоты облойной канавки h к высоте канавки H
В случае линейной зависимости между xи С коэффициент r = ± 1, при полном отсутствии связи r=0.
При решении вопроса: будет ли вычисленный коэффициент корреляции r указывать на какую-либо корреляцию между х и С, применяется критерий Стьюдента
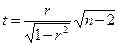 ,
,
откуда 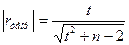 . (5)
. (5)
Значения t находят из таблиц, согласно принятому уровню значимости, и числу степеней свободы f = п — 2 . Если полученное по уравнению (5) значение r будет меньше расчетного, то можно утверждать наличие зависимости между случайными переменными х и С.
При исследовании более двух случайных величин применяется метод математической статистики, называемый множественной корреляцией. Особенность и преимущества этого метода заключаются в том, что его применение не требует проведения специальных лабораторных исследований, когда в целях, изучения влияния одного фактора стремятся остальные факторы оставить без изменения. Для применения метода множественной корреляции вариация многочисленных факторов не представляет какой-либо трудности, поэтому указанный метод является наиболее эффективной формой исследования закономерностей разрушения инструмента в реальных, производственных условиях.
Для определения совместного влияния факторов вычисляют коэффициент множественной корреляции
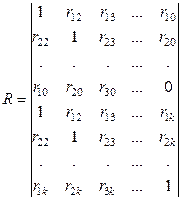
Здесь индексы от «1» до k означают параметры инструмента, а индекс «0» — стойкость (например, r10 - коэффициент корреляции со стойкостью первого параметра).
Матрицы решаются согласно правилам линейной алгебры. Отсюда cледует, что для двух переменных x1 и х2 коэффициент R рассчитывается по формуле
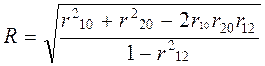
При независимых переменных, т. е. при r12 = 0
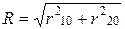
По этой же формуле подсчитывается Ri в том случае, когда имеется Ri-1 для i-1 параметров и необходимо найти Rt при включении i-го параметра, теснота связи которого r10:
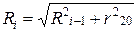
Стойкостные испытания инструмента являются весьма трудоемкими. Они требуют больших затрат времени, значительных материальных затрат на изготовление инструмента и на материал для проведения эксперимента. Поэтому весьма актуальным является расчет стойкости на основе метода планирования многофакторного эксперимента.
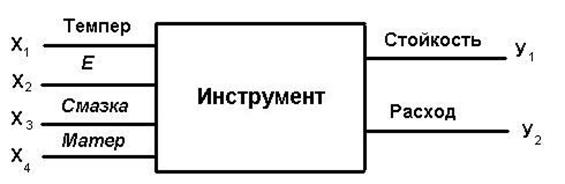
Рисунок 11 - Блок-схема эксплуатации штампа
в процессе горячей штамповки
Поставленная задача решается на основе представления о кибернетической системе, которую называют «чёрным ящиком» (рисунок 11). Он представляет собой систему связей, недоступную для наблюдения, так как о содержании, механизме процесса нам ничего не известно или известно лишь частично: известны только входы, переменные х, участвующие в процессе (факторы), и выходы — результат процесса (параметр оптимизации), обозначенный символом у.
Каждый фактор может принимать в опыте одно или несколько значений. Такие значения называются уровнями. Схема «черного ящика» позволяет строить математические уравнения, связывающие параметр оптимизации с факторами: y=f(x1,x2,... ...,Xk). Задача эксперимента состоит в том, чтобы определить численные значения коэффициентов этого уравнения. Обычно функцию f(x1, x2,..., xk) выбирают в виде степенного ряда. В частности, для двух факторов функция имеет вид полиномов первой степени y=b0+b1x1+b2x2; с неполным квадратным членом: y=b0+b1x1+b2x2+b12x1x2
Модель должна быть достаточно точной, т. е. близкой к фактической зависимости. Тогда считают, что она адекватна.
При планировании по схеме полного факторного эксперимента реализуются все возможные комбинации факторов на всех выбранных для исследования уровнях. Необходимое количество опытов N при полном факторном эксперименте определяется по формуле N = pk, где р — количество уровней; k — число факторов.
Если эксперименты проводятся на двух уровнях, то постановка опытов по такому плану называется полным факторным экспериментом типа 2k. Каждый фактор, участвующий в процессе, имеет определенный предел изменения своей величины. Совокупность всех значений, которые принимает фактор называется областью определения фактора. Но в области определения надо найти локальную подобласть для планирования эксперимента, т. е. для каждого фактора необходимо указать тот интервал изменения параметров, в пределах которого проводятся исследования. Для этого на основании априорной информации устанавливают ориентировочно значения факторов, комбинации которых дают наилучший результат. Этой комбинации значений факторов соответствует многомерная точка в факторном пространстве, которую принимают за исходную при построений плана эксперимента. Координаты этой точки называются основными уровнями факторов.
После того как основной уровень выбран, переходят к следующему шагу — выбору интервалов варьирования. Интервалом варьирования фактора называется некоторое число, прибавление которого к основному уровню дает верхний, а вычитание — нижний уровень фактора.
Поскольку факторы изучаемого процесса неоднородны и имеют различные единицы измерения, их следует привести к единой системе исчисления путем переходу от действительных значений факторов к кодированным по формуле 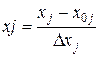 , где xj — кодированное значение фактора; хj — натуральное значение фактора; х0j — натуральное значение фактора на основном уровне; j — номер фактора;
, где xj — кодированное значение фактора; хj — натуральное значение фактора; х0j — натуральное значение фактора на основном уровне; j — номер фактора; 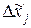 - интервал варьирования.
- интервал варьирования.
В безразмерной системе координат верхний уровень равен «+1», нижний соответственно «—1», координаты основного уровня равны нулю. Для случая N = 22 условия проведения эксперимента записывают в виде таблицы, которую называют матрицей планирования эксперимента (таблица 1).
Построение матриц планирования основано на правиле чередования знаков: в первом столбце они меняются поочередно, во втором чередуются через два, в третьем — через четыре и т. д., по степеням двойки.
Таблица 1 - Матрица планирования эксперимента 22
| Номер опыта | x0 | x1 | x2 | y |
| + | - | - | y1 | |
| + | + | - | y2 | |
| + | - | + | y3 | |
| + | + | + | y4 |
По результатам эксперимента определяются коэффициенты математической модели:
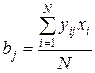 (6)
(6)
Чтобы привести процедуру вычисления коэффициента b0 в соответствие с формулой (6), в матрицу планирования введем, столбец фиктивной х0, которая во всех опытах принимает значение «+1». Коэффициенты при независимых переменных указывают на силу влияния факторов. Чем больше" численная величина коэффициента bj, тем большее влияние оказывает фактор. Если коэффициент имеет знак «+», то с увеличением значения фактора у исследуемый параметр увеличивается, а если «-», то уменьшается.
Планируя эксперимент, мы стремимся получить линейную модель, однако у нас нет уверенности в том, что в выбранных интервалах варьирования процесс описывается линейной моделью. Один из часто встречающихся видов нелинейности связан с тем, что эффект (влияние) одного фактора зависит от уровня, на котором находится другой фактор. Полный факторный эксперимент позволяет количественно оценивать эффекты взаимодействия. Для этого следует, пользуясь правилом перемножения столбцов, получить столбец произведения двух факторов (таблица 2).
Таблица 2 - Матрица планирования эксперимента 22 с эффектом взаимодействия
| Номер опыта | х0 | х1 | х2 | х1,х2 (х3) | у |
| + + + + | - + - + | - - + + | + - - + | у1 у2 у3 у4 |
Математическая модель выглядит следующим образом:
у=b0+b1x1+b2x2+b12x1x2
Коэффициент b12 вычисляется аналогично о формуле (2). Каждый эксперимент содержит элемент неопределенности вследствие ограниченности информации. Параллельные опыты не дают полностью совпадающих результатов, потому что всегда существует ошибка опыта (ошибка воспроизводимости). Для ее определения опыт воспроизводится по возможности в одинаковых условиях несколько раз, а затем берется среднее арифметическое всех результатов: 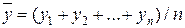 , где n — число параллельных опытов. Отклонение результата любого опыта от среднего арифметического можно представить как разность
, где n — число параллельных опытов. Отклонение результата любого опыта от среднего арифметического можно представить как разность 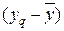 , где yq – результат отдельного опыта. Наличие отклонений свидетельствует об изменении значений, полученных при повторных опытах. Для измерения этого различия чаще всего используют дисперсию опыта, описываемую уравнением
, где yq – результат отдельного опыта. Наличие отклонений свидетельствует об изменении значений, полученных при повторных опытах. Для измерения этого различия чаще всего используют дисперсию опыта, описываемую уравнением
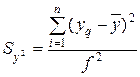 ,
,
где f— число степеней свободы — понятие, учитывающее в статистических ситуациях связи, ограничивающие свободу изменения случайных величин. Значение f подсчитывается как разность между числом выполненных опытов и числом констант (коэффициентов, средних и т.д.), подсчитанных по результатам тех же опытов. В данном случае f=n-1, так как на вычисление у расходуется одна степень свободы.
Для расчета Sy2 опыты, заданные матрицей планирования, дублируют n раз и подсчитывают построчные дисперсии:

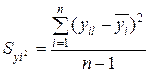
где уil— результат параметра оптимизации l-го повторения i- го опыта,
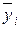 - среднее арифметическое значение всех повторений i-го опыта,
- среднее арифметическое значение всех повторений i-го опыта,
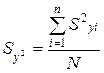 ,
,
т. е. ставится серия одинаковых опытов n, затем проверяется однородность дисперсий, т. е. выясняется; определяются ли различные значения у с одинаковой точностью по критерию Кохрена:

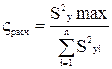 .
.
Расчетное значение ( 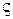 -критерия сравнивает её с табличным в зависимости от уровня значимости
-критерия сравнивает её с табличным в зависимости от уровня значимости 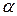 , числа степеней свободы t = n— 1 и числа опытов N. Ряд дисперсий считается однородным, если
, числа степеней свободы t = n— 1 и числа опытов N. Ряд дисперсий считается однородным, если 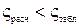 .
.
Уровень значимости 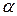 — мера точности ответа. Для инженерных расчетов подходящим является
— мера точности ответа. Для инженерных расчетов подходящим является 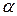 = 0,05, что соответствуем вероятности правильного ответа: р=1—
= 0,05, что соответствуем вероятности правильного ответа: р=1— 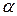 = 0,95 или 95%. При этом считают, что в среднем в 5% случаев возможна ошибка.
= 0,95 или 95%. При этом считают, что в среднем в 5% случаев возможна ошибка.
Коэффициенты модели bj -считаются значимыми, когда их абсолютная величина больше доверительного интервала, т. е.; где t — критерий Стьюдента (берется из таблиц в зависимости от уровня значимости а и числа степеней свободы при определении дисперсии опыта, Sbj— среднеквадратичная ошибка определения коэффициентов регрессии, Sbi2 = Sy2/hN — дисперсия в определении коэффициентов.
Статистическая незначимость коэффициента интерпретируется как отсутствие влияния соответствующего фактора в изученных интервалах его измерения. Такие коэффициенты из модели исключаются.
Адекватность модели проверяют с помощью критерия Фишера:
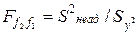
где 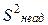 — дисперсия неадекватности,
— дисперсия неадекватности, 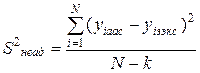
Здесь уiрасч, уiэксп — значения параметра оптимизации в i-м опыте, соответственно рассчитанные по уравнению регрессии и определенные экспериментально, k — число коэффициентов уравнения регрессии, включая bо.
Гипотеза об адекватности уравнения принимается в том случае, когда рассчитанное значение F- критерия не превышает табличного для выбранного уровня значимости и числа степеней свободы f1 и f2, с которыми определялись дисперсии неадекватности и опыта, т.е. Fрасч£F.
РАЗГАРНЫЕ ТРЕЩИНЫ
Дата добавления: 2015-12-10; просмотров: 1117;
