Основные виды и факторы разрушения инструмента
Требования, предъявляемые к деформирующему инструменту
1. Обеспечение точной конфигурации и размеров изделия;
2. Долговечность и надежность в работе;
3. Инструмент должен быть дешевым в изготовлении;
4. Инструмент должен быть технологичным в изготовлении.
СТОЙКОСТЬ ИНСТРУМЕНТА
Понятие стойкости
Стойкость инструмента является случайной переменной величиной, которая может принимать для одного и того же инструмента в одинаковых условиях эксплуатации различные значения. Эта величина определяется качеством инструмента, которое создается в процессе изготовления определенной совокупностью физико-механических, конструктивных и геометрических параметров и условиями эксплуатации (свойством обрабатываемого материала, режимами обработки и т. д.). Влияние этих факторов на стойкость различно по силе и направлению. Указанные условия определяют стойкость как случайную переменную величину. Обычно для характеристики величины стойкости пользуются некоторым ее средним значением
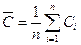 , где n — общее число испытаний. Однако значение среднего арифметического не является полной характеристикой случайной переменной величины. Практика эксплуатации показывает, что значение средней стойкости не позволяет рассчитать, например, период принудительной замены инструмента, его надежность, оценку нового варианта изготовления инструмента и т. п. Случайная величина полностью описывается, если задан закон ее распределения, т. е. имеется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями.
, где n — общее число испытаний. Однако значение среднего арифметического не является полной характеристикой случайной переменной величины. Практика эксплуатации показывает, что значение средней стойкости не позволяет рассчитать, например, период принудительной замены инструмента, его надежность, оценку нового варианта изготовления инструмента и т. п. Случайная величина полностью описывается, если задан закон ее распределения, т. е. имеется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями.
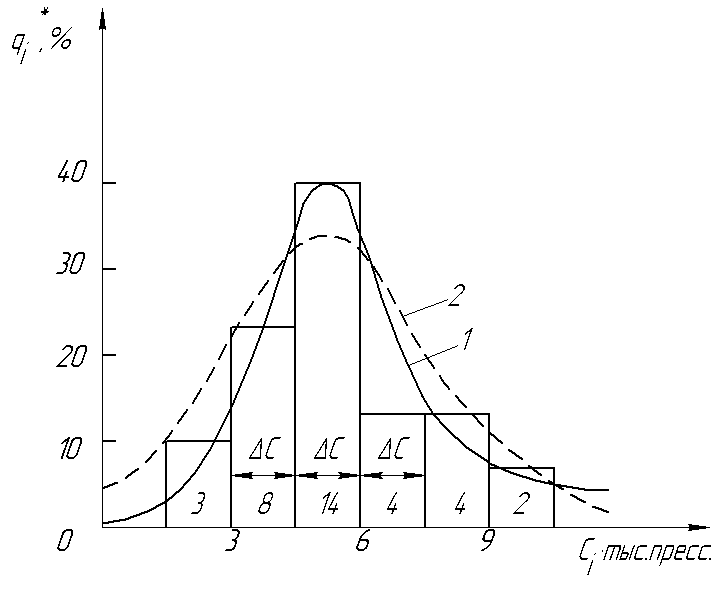
Рисунок 2 - Гистограмма с наложенными кривыми
эмпирического (1) и нормального (2) распределений стойкости инструмента
Для исследования закона распределения стойкости деформирующего инструмента в реальных условиях наиболее доступным является статистический метод, на основании которого проводится серия испытаний п. Полученные значения стойкости группируют в интервалах 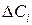 , где i — номер интервала. Число интервалов N должно быть не менее 6—7. Чтобы определить величину интервала
, где i — номер интервала. Число интервалов N должно быть не менее 6—7. Чтобы определить величину интервала 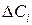 , вначале находят максимальное Смакс и минимальное Смин значения стойкости в серии испытаний и, задавшись числом интервалов N, находят
, вначале находят максимальное Смакс и минимальное Смин значения стойкости в серии испытаний и, задавшись числом интервалов N, находят 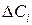 = (Смакс—Cмин)/N. Потом по оси абсцисс откладывают равные интервалы длиной
= (Смакс—Cмин)/N. Потом по оси абсцисс откладывают равные интервалы длиной 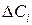 и подсчитывают число инструментов, попадающих в каждый из этих интервалов (рисунок 2). По количеству инструментов в каждом интервале ni определяют частоту рассеяния (плотность распределения)
и подсчитывают число инструментов, попадающих в каждый из этих интервалов (рисунок 2). По количеству инструментов в каждом интервале ni определяют частоту рассеяния (плотность распределения) 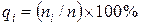 . По оси ординат откладывают значения плотности распределения qi, в соответствующих интервалах. Так как значения qi приняты, равными для всего интервала
. По оси ординат откладывают значения плотности распределения qi, в соответствующих интервалах. Так как значения qi приняты, равными для всего интервала 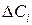 , то получают диаграмму в виде прямоугольников с шириной, равной интервалу
, то получают диаграмму в виде прямоугольников с шириной, равной интервалу 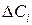 , называемую в теории математической статистики гистограммой. Если диаграмму изобразить в виде плавной - линии, соединяющей последовательно между собой значения плотности распределения, то получают график эмпирического закона стойкости (рисунок 2, кривая 1).
, называемую в теории математической статистики гистограммой. Если диаграмму изобразить в виде плавной - линии, соединяющей последовательно между собой значения плотности распределения, то получают график эмпирического закона стойкости (рисунок 2, кривая 1).
Анализ результатов большого объема производственных испытаний формоизменяющего инструмента показывает, что эмпирическое распределение стойкости хорошо согласуется с теоретической кривой нормального распределения Гаусса, происходит это в том случае, когда на стойкость инструмента действует несколько факторов и среди них нет преобладающего (наиболее благоприятный случай):
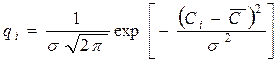
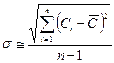
где 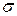 - среднеквадратичное отклонение стойкости,
- среднеквадратичное отклонение стойкости,
В дальнейшем проводят сравнение эмпирического распределения стойкости с нормальным распределением стойкости Гаусса и определяют их возможное совпадение. Для этого рассчитывают параметры теоретического распределения по формуле
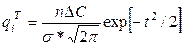 ,
, 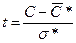
где 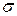 * и С* определяют по данным серии испытаний. Функция
* и С* определяют по данным серии испытаний. Функция 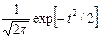 табулирована. На основе полученных данных строят теоретическую кривую нормального распределения (рисунок 2, кривая 2).
табулирована. На основе полученных данных строят теоретическую кривую нормального распределения (рисунок 2, кривая 2).
Существует несколько способов проверки эмпирического распределения на нормальность.
Одним из быстрых и простых способов проверки на нормальность распределения является способ В. И. Романовского, согласно которому, если
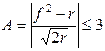 ,
,
то гипотеза принимается. Если А > 3, то гипотеза о согласовании бракуется.
Критерий f вычисляется по формуле
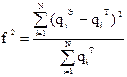
где 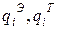 — соответственно эмпирические и теоретические плотности распределения для i-ro интервала;
— соответственно эмпирические и теоретические плотности распределения для i-ro интервала;
r — число степеней свободы, r=n — р — 1;
р— число параметров в теоретическом распределении (для нормального закона р=2).
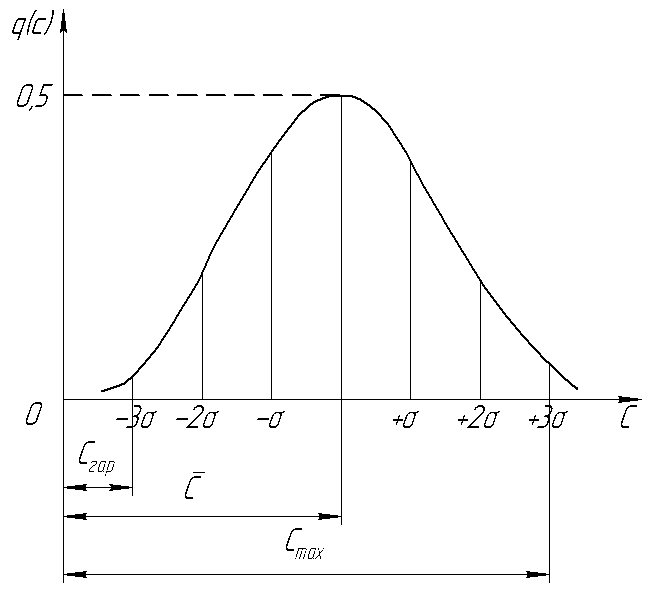
Рисунок 3 - Средняя 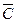 , гарантированная Сгар и максимальная Смакс стойкости инструментов.
, гарантированная Сгар и максимальная Смакс стойкости инструментов.
Другой способ проверки - с помощью вероятностной бумаги. Для этого строят график в координатах: стойкость инструмента по оси абсцисс и вероятность того что стойкость инструмента не превышает заданную по оси ординат. Последнее рассчитывают по формуле:
q*=n*/n х 100%,
Если построенные точки на графике образуют линию, проходящую через точку с координатами 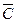 и q*=50 %, то гипотеза принимается.
и q*=50 %, то гипотеза принимается.
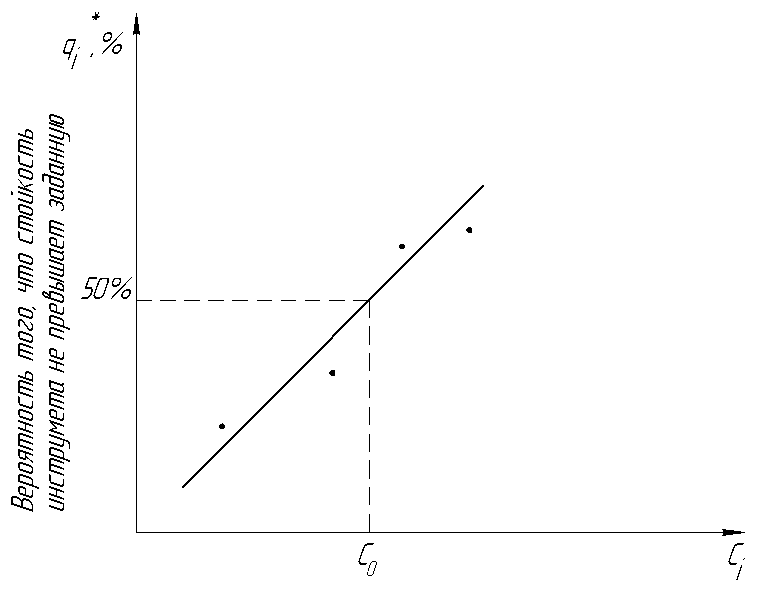
Рисунок 4 - График проверки нормальности распределения стойкости с помощью метода вероятностной бумаги
Согласование теоретической и эмпирической кривых означает, что для анализа стойкости деформирующего инструмента можно использовать теоретическую кривую нормального распределения. В пределах доверительного интервала 3 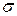 в ту и другую сторону от
в ту и другую сторону от 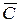 расположено 99,7% всех возможных значений стойкости, в связи с чем нетрудно вычислить гарантированную Crap =
расположено 99,7% всех возможных значений стойкости, в связи с чем нетрудно вычислить гарантированную Crap = 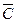 —3
—3 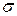 и максимальную Смакc =
и максимальную Смакc = 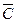 +3
+3 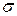 стойкости (рисунок 3). Средней стойкости
стойкости (рисунок 3). Средней стойкости 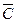 соответствует вероятность, равная 0,5, т. е. одинаково вероятно, что стойкость инструмента окажется больше и что она будет меньше.
соответствует вероятность, равная 0,5, т. е. одинаково вероятно, что стойкость инструмента окажется больше и что она будет меньше.
Вид кривой эмпирического закона распределения стойкости позволяет наметить пути повышения стойкости деформирующего инструмента. При нормальном законе распределения стойкости деформирующего инструмента ни один из многочисленных случайных факторов не доминирует над остальными, т. е. не играет преобладающей роли. В таких случаях повысить стойкость инструмента можно только комплексно, путем комбинации различных приемов (изменение конфигурации инструмента, замена материала, охлаждение и т; д.).
На рис. 5 показаны возможные виды эмпирических кривых распределения стойкости, отличных от нормального распределения.
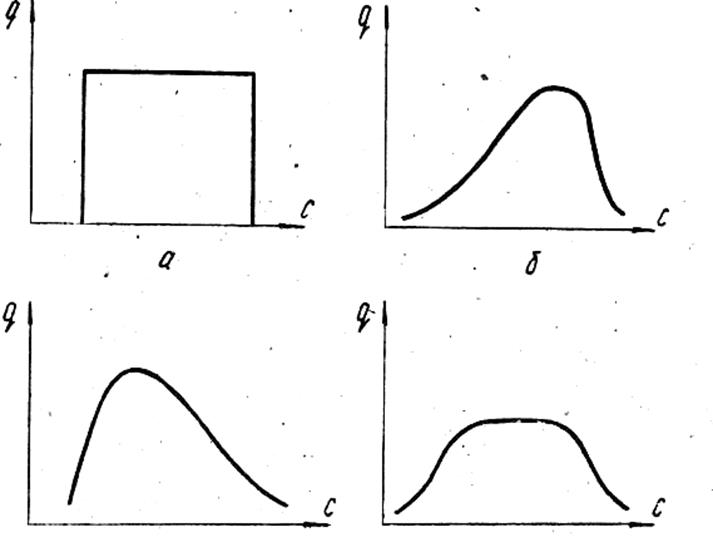
Рисунок 5 - Виды эмпирических законов распределения стойкости в реальных условиях: а — закон равной вероятности, б — композиция закона Гаусса и равномерно возрастающей вероятности, в — экспоненциальный закон, г — композиция Гаусса и закон равной вероятности.
В случае, когда кривая (рисунок 5, а) близка к закону равной вероятности, на стойкость инструмента оказывает влияние резко доминирующий фактор, например, равномерно изменяющийся во времени износ. Уменьшение влияния этого фактора позволяет повысить стойкость инструмента. Наряду с множеством случайных факторов, задающих в совокупности нормальный закон (рисунок 5, б), на стойкость инструмента оказывает влияние фактор, замедленно изменяющийся во времени, например, разогрев инструмента за счет теплового эффекта. Если часть изготовленного инструмента имеет грубые технологические дефекты (низкое качество термообработки, дефекты материала инструмента), то в результате испытаний стойкость дефектного инструмента будет меньше, чем у остального, и кривая эмпирического распределения будет близкой к экспоненциальному распределению (рисунок 5,в). На рисунке 5,г представлен закон, по которому, наряду с множеством случайных факторов, дающих в совокупности нормальное распределение, на стойкость инструмента оказывает влияние преобладающий фактор, равномерно изменяющийся во времени.
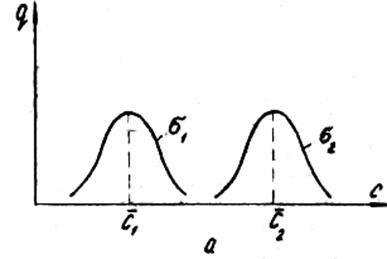
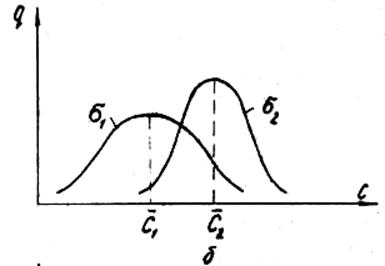
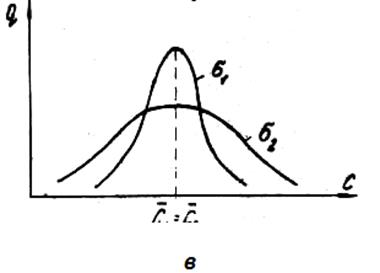
Рисунок 6 - Сравнение альтернативных вариантов инструмента, имеющих различные
значения средней стойкости среднеквадратичного отклонения
Эмпирические законы распределения стойкости могут быть полезными при сопоставлении альтернативных вариантов деформирующего инструмента, отличающихся друг от друга по технологии изготовления, материалами, способами упрочнения поверхности, конфигурацией и т. п. Из рисунка 6, а видно, что средняя стойкость может служить критерием выбора оптимального варианта, так как С2> С1+ 3 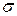 1. Для случая на рисунке 6, б возникает вопрос: существенно ли различие между С1 И С2 или оно носит случайный характер. Ответ на этот вопрос можно получить, сравнив средние значения стойкости инструмента с помощью критерия Стьюдента. Если число испытаний п < 25, то используем формулу
1. Для случая на рисунке 6, б возникает вопрос: существенно ли различие между С1 И С2 или оно носит случайный характер. Ответ на этот вопрос можно получить, сравнив средние значения стойкости инструмента с помощью критерия Стьюдента. Если число испытаний п < 25, то используем формулу
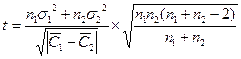
где n1 и n2 – число испытаний старого и нового вариантов соответственно;
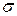 1 и
1 и 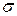 2 – эмпирические дисперсии в первой и второй сериях.
2 – эмпирические дисперсии в первой и второй сериях.
Если в результате расчетов оказывается, что, │ 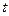 │ ≥ tкр то
│ ≥ tкр то 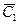 и
и 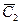 различаются существенно. Если, │
различаются существенно. Если, │ 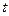 │ < tкр то расхождение носит случайный характер. Значение tкp находят по таблице работы при f = п1 + п2 — 2 и уровне значимости
│ < tкр то расхождение носит случайный характер. Значение tкp находят по таблице работы при f = п1 + п2 — 2 и уровне значимости 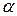 = 0,05.
= 0,05.
Пример расчета. Шестнадцать матриц, изготовленных по новой технологии, проработали до разрушения в среднем 150 дней, среднеквадратичное отклонение составило 25 дней. Десять матриц, изготовленных по старой технологии, проработали до разрушения в среднем 120 дней, их среднеквадратичное отклонение составило 12 дней. Определить, является ли новая технология с точки зрения стойкости лучше, чем старая, по формуле
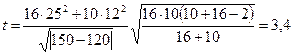
По таблице из работы для f = 10 + 16—2 = 24 и 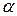 = 0,05, tкр = 2,064, что меньше вычисленного. Следовательно, различие в значениях средней стойкости существенно, и новая технология с точки зрения стойкости лучше. На рисунке 6,в распределение, отображенное кривой 2, имеет больший диапазон, чем распределение, отображенное кривой 1. Более качественным является инструмент, стойкость которого описывается кривой 1, так как обеспечивает незначительный риск и большую стабильность величин стойкости.
= 0,05, tкр = 2,064, что меньше вычисленного. Следовательно, различие в значениях средней стойкости существенно, и новая технология с точки зрения стойкости лучше. На рисунке 6,в распределение, отображенное кривой 2, имеет больший диапазон, чем распределение, отображенное кривой 1. Более качественным является инструмент, стойкость которого описывается кривой 1, так как обеспечивает незначительный риск и большую стабильность величин стойкости.
Чтобы получить закон распределения стойкости инструмента, иногда целесообразно использовать модели накапливающихся и мгновенных повреждений. Будем считать выход инструмента из строя в результате накопления, повреждений, получаемых в случайные моменты процесса деформирования. Повреждение — редкое событие, и поэтому можно принять, что число повреждений m следует закону распределения редких событий - закону Пуассона.
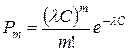 , m = 0, 1, 2, …,
, m = 0, 1, 2, …,
где Pm - получения m - повреждений при заданной стойкости
инструмента С;
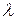 - интенсивность «потока повреждений», например среднее число повреждений, приходящихся на прокатку единицы массы металла.
- интенсивность «потока повреждений», например среднее число повреждений, приходящихся на прокатку единицы массы металла.
Пусть инструмент выходит из строя после получения S повреждений. Тогда плотность вероятности распределения
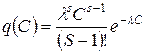 (1)
(1)
следует закону гамма-распределения.
Такие вероятностные модели строят для оценки стойкости прокатных валков. При этом под стойкостью С понимают массу металла, прокатанного до выхода валков из строя.
Если имеется грубое нарушение хода процесса прокатки (S=1), то формула (1) приобретает вид 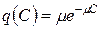 с. Здесь вместо
с. Здесь вместо 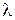 интенсивность обозначена через
интенсивность обозначена через 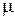 , чтобы подчеркнуть, что речь идет о внезапных повреждениях. Таким образом, распределение стойкости валков при внезапных повреждениях следует показательному закону.
, чтобы подчеркнуть, что речь идет о внезапных повреждениях. Таким образом, распределение стойкости валков при внезапных повреждениях следует показательному закону.
Валки подвергаются разрушению как в результате накопления повреждений (происходит постепенное изменение состояния валков), так и при внезапных повреждениях, например порез валков при прокатке. В последнем случае распределение стойкости валков представляет собой суперпозицию распределений (1) с различными S и 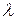 (q®C):
(q®C):
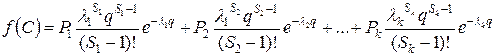 , (2)
, (2)
где Р1, Р2, …, Рk - доля отдельных распределений, образующих итоговые распределения (P1 + Р2+.. + Рk = 1).
Рассмотрим наряду с формулой (2) запись гамма-распределения в общем виде:
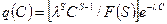 (3)
(3)
где F(C) – гамма-функция от S.
Если под S и X в формуле (3) понимать средние значения соответствующих величин в формуле (2), то выражение (3) удовлетворительно аппроксимирует распределение (2). Для определения по экспериментальным данным параметров гамма-распределения (3) удобно пользоваться методом моментов, согласно которому
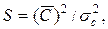
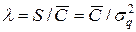 ,
,
где 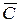 и
и 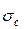 - среднее значение и среднее квадратичное отклонение эмпирического ряда распределения С.
- среднее значение и среднее квадратичное отклонение эмпирического ряда распределения С.
Исходя из знания закона распределения стойкости, можно дать определения стойкости и надежности инструмента.
Стойкость деформирующего инструмента — это количество изготовленных изделий требуемого качества в условиях нормального функционирования инструмента при заданной вероятности выхода его из строя:
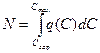
Надежность деформирующего инструмента — это вероятность функционирования при выполнении программы производства М
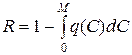
Единицы измерения стойкости инструмента различаются по видам обработки металлов давлением. Так, стойкость инструмента при прессовании определяется количеством прессовок; при прокатке и волочении — весовыми или линейными единицами; при горячей «холодной штамповке — количеством штампоударов. В некоторых случаях в качестве меры стойкости используется время работы инструмента.
Основные виды и факторы разрушения инструмента
Основными видами разрушения инструмента являются необратимые деформации, разгарные трещины и износ. Все перечисленные виды в большей или меньшей степени взаимодействуют друг с другом в процессе разрушения инструмента. Однако для каждого конкретного типа инструмента, для отдельных элементов деформирующей поверхности выделяют в качестве преобладающего один из перечисленных видов разрушений. Преобладание одного вида разрушения над другим зависит от взаимодействия множества факторов.
До сих пор не существует" единого мнения относительно характера и значимости влияния различных факторов на виды разрушения инструмента в процессе его изготовления и эксплуатации Б. Ф. Трахтенберг все факторы, влияющие на стойкость инструмента, делит на четыре группы: металлургические, технологические, конструктивные и эксплуатационные [3]. К группе металлургических факторов относится химический состав материала, инструмента и способ изготовления заготовки для инструмента. Конструктивные факторы включают метод деформирования, размеры и форму инструмента. К технологическим факторам - относят способы изготовления, термической обработки, упрочнения и т. д. Эксплуатационные факторы включают температуру деформирования, степень деформации, вид смазки, условия подогрева инструмента и т. д.
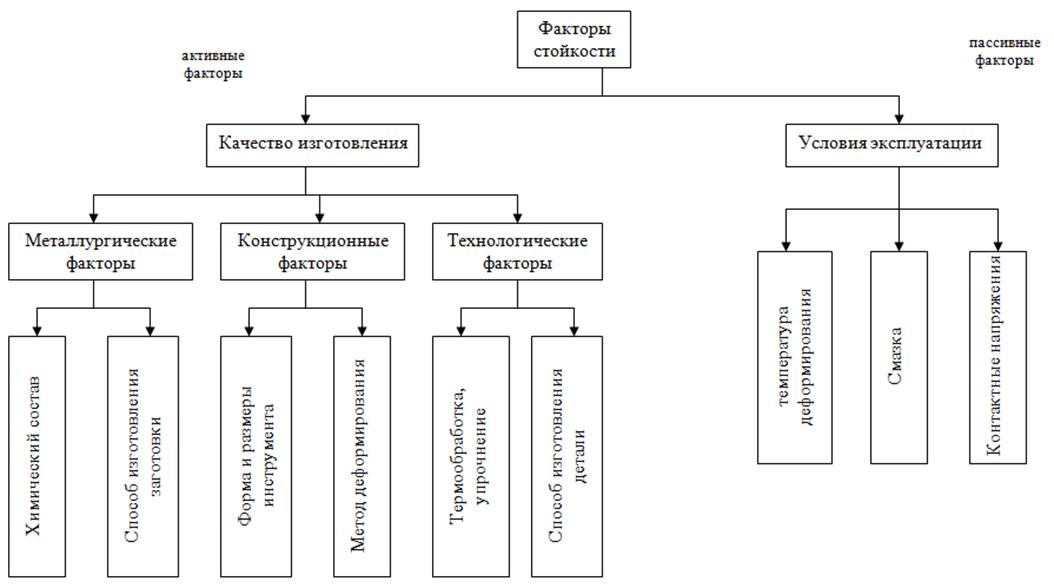
Рисунок 7 - Факторы стойкости деформирующего инструмента
С. А. Довнар на основе производственного опыта все доминирующие факторы, влияющие на стойкость, представил в виде схемы (рисунок 8). Кроме того, следует отметить влияние таких субъективных факторов, как культура производства, квалификация рабочих, соблюдение ими технологических инструкций.
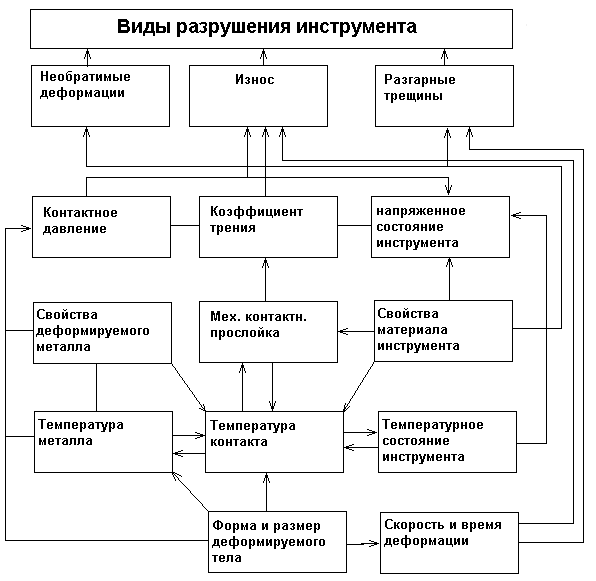
Рисунок 8 - Схема доминирующих факторов разрушения инструмента
Многообразие факторов, действующих в процессе эксплуатации инструмента, осложненное их взаимодействием, не поддающимся теоретическому анализу, и отсутствие достаточных экспериментальных данных об условиях работы инструмента затрудняет разработку эффективных мероприятий по повышению его стойкости.
Дата добавления: 2015-12-10; просмотров: 1867;
