Швидкість точок у складному русі

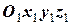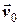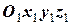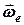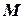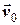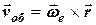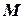Розглянемо систему відліку , що рухається відносно основної системи (рис. 6.1). Якщо система рухається поступально зі швидкістю по відношенню до основної системи та обертається з кутовою швидкістю , то лінійна швидкість переносного руху точки має дві складові – (швидкість поступального руху) та (швидкість обертального руху, де - радіус вектор точки відносно довільної точки на осі обертання рухомої системи відліку). У цьому випадку для швидкості переносного руху точки 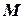отримуємо

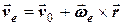. (6.1)

Якщо точка 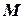рухається зі швидкістю 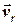відносно рухомої системи координат тоді для абсолютної швидкості точки 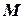отримуємо

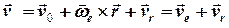(6.2)

Отже, абсолютна швидкість точки в складному русі дорівнює векторної сумі швидкості відносного руху 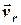та швидкості переносного руху в даній точці рухомої системи .

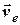Виходячи з того, що абсолютна швидкість точки визначається діагоналлю паралелограма побудованого на векторах 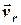і 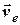(рис. 6.1), модуль абсолютної швидкості точки можна знайти скориставшись теоремою косинусів

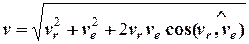. (6.3)

У відсутності обертального руху переносника формула (6.2) спрощується до

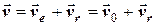. (6.4)

Розглянемо корисний приклад застосування законів складного руху на практиці. Так, у відсутності течії, судно під дією двигуна рухається істинним курсом 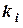(напрям за компасом) зі швидкістю 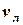, яку забезпечує двигун відносно нерухомого водного середовища (лагова швидкість). Якщо воно попадає в область, де діє течія, швидкість якої відома 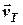, то вектор абсолютної (шляхової) швидкості судна буде визначатися векторною сумою швидкості течії 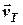та лагової швидкості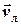

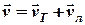, (6.5)

а величина абсолютної швидкості 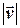та шляховий напрям буде відрізнятися від 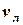та .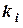

Прискорення точок у складному русі

Для знаходження абсолютне прискорення точки, тобто її прискорення по відношенню до основної системи координат беремо похідну від правої та лівої частини формули (6.3) і отримуємо

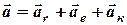, (6.6)

отже, абсолютне прискорення дорівнює геометричній сумі прискорень відносного 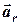, переносного 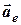та Коріоліса .

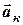Вектор відносного прискорення точки, тобто прискорення точки по відношенню до рухомої системи координат

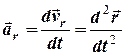. (6.7)

Вектор переносного прискорення, тобто прискорення, зумовленого рухом системи

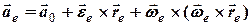, (6.8)

де 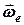та – кутова швидкість та кутове прискорення переносника відповідно, складається з векторів

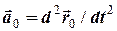(6.9)

- поступального прискорення переносника (початку рухомої системи координат – точки ),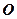

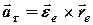(6.10)

- тангенціального (обертального) прискорення точки М сумісно з переносником,

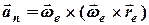(6.11)

- нормального прискорення точки М відносно миттєвої осі обертання.

Останній доданок в (7.2) – прискорення Коріоліса, яке обумовлено взаємним впливом переносного та відносних рухів і характеризує зміну напряму відносної швидкості, викликаної переносним рухом, та зміну величини переносної швидкості за рахунок відносного руху

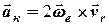. (6.12)

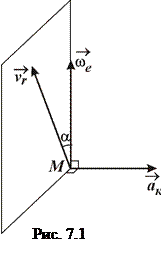
Напрям вектора прискорення Коріоліса (рис. 7.1) визначається згідно з правилом векторного добутку векторів 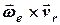, а його модуль дорівнює

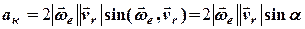. (6.13)

Прискорення Коріоліса відсутнє в ті моменти, коли:

1) 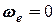, тобто коли переносний рух є чисто поступальним;

2) 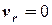, тобто точка не рухається відносно рухомої системи відліку;

3) 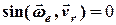, тобто вектори 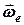i 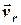колінеарні.

Контрольні запитання

1 Який рух точки називається складним?

2 Який рух називають відносним? переносним? абсолютним?

3 Який зв’язок існує між абсолютною, переносною та відносною швидкостями точки?

4 Запишіть формулу для визначення абсолютного прискорення точки при її складному русі та поясніть кожний доданок.

5 Дайте визначення прискорення Коріоліса. Від яких величин воно залежить? В яких випадках прискорення Коріоліса дорівнює нулю?

6 В яких точках Землі та як повинно рухатись судно з незмінною величиною швидкості, щоб прискорення Коріоліса: а) дорівнювало нулю?
б) мало найбільше значення?