Момент сили відносно точки
Моментом сили 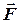 відносно точки
відносно точки 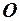 називається фізична величина, яка характеризує здатність сили викликати обертальній рух тіла відносно даної точки і визначається векторним добутком векторів
називається фізична величина, яка характеризує здатність сили викликати обертальній рух тіла відносно даної точки і визначається векторним добутком векторів  та
та 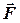
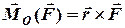 (3.1)
(3.1)
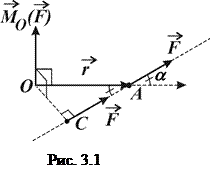 де
де  – вектор, проведений з даної точки
– вектор, проведений з даної точки 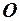 у точку
у точку 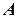 прикладання сили. Згідно з властивостями векторного добутку вектор
прикладання сили. Згідно з властивостями векторного добутку вектор 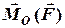 перпендикулярний площині, в якій лежать вектори
перпендикулярний площині, в якій лежать вектори  та
та 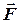 (рис. 3.1) та його модуль
(рис. 3.1) та його модуль
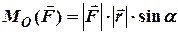 . (3.2)
. (3.2)
Модуль моменту сили залежить від орієнтації векторів  та
та 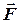 , має макси-мальне значення
, має макси-мальне значення 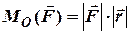 , коли вектори перпендикулярні і дорівнює нулю коли вони паралельні, тобто лінія дії сили проходить через точку
, коли вектори перпендикулярні і дорівнює нулю коли вони паралельні, тобто лінія дії сили проходить через точку 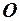 . Момент сили вимірюється в ньютоно-метрах.
. Момент сили вимірюється в ньютоно-метрах.
Сила 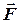 є ковзний вектор, тому момент сили відносно точки не змінюється при переміщенні точки прикладання сили вздовж лінії її дії, наприклад, коли силу
є ковзний вектор, тому момент сили відносно точки не змінюється при переміщенні точки прикладання сили вздовж лінії її дії, наприклад, коли силу 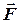 перенести з точки
перенести з точки 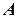 в точку
в точку 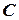 (рис. 3.1).
(рис. 3.1).
Вкажемо різні способи знаходження вектора моменту сили. В площині, де лежать вектори  та
та 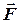 введемо декартову систему координат
введемо декартову систему координат  , сумістивши початок координат з точкою
, сумістивши початок координат з точкою 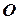 (рис.3.2) .
(рис.3.2) .
1. З точки 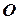 проведемо перпендикуляр на лінію дії сили (рис. 3.2а). Від-стань
проведемо перпендикуляр на лінію дії сили (рис. 3.2а). Від-стань 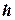 від заданої точки
від заданої точки 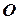 до лінії дії сили називається плечем
до лінії дії сили називається плечем
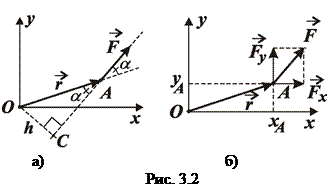
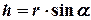 . (3.3)
. (3.3)
Для визначення напряму можливого обертання твердого тіла під дією сили навколо заданої точки замість вектора моменту, який перпендикулярний площині  , використовують його алгебраїчне значення
, використовують його алгебраїчне значення
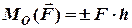 , (3.4)
, (3.4)
яке визначається добутком модуля сили на плече. Знак плюс береться, коли сила викликає обертання тіла навколо точки 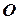 проти напряму руху стрілки годинника (тоді вектор
проти напряму руху стрілки годинника (тоді вектор 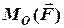 напрямлений до нас) і мінус – коли за напрямом руху стрілки годинника (тоді вектор
напрямлений до нас) і мінус – коли за напрямом руху стрілки годинника (тоді вектор 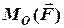 напрямлений від нас). Взаємна орієнтація векторів
напрямлений від нас). Взаємна орієнтація векторів  та
та 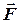 , що зображена на рис. 3.2а, відповідає випадку
, що зображена на рис. 3.2а, відповідає випадку 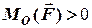 .
.
3. Зручно знаходити момент сили відносно точки використовуючи теорему Варіньона. Для цього силу 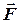 розкладають на складові
розкладають на складові 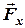 та
та 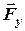 і визначають алгебраїчне значення моменту, як суму моментів, які створюють ці складові відносно точки
і визначають алгебраїчне значення моменту, як суму моментів, які створюють ці складові відносно точки 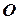 (рис.3.2б)
(рис.3.2б)
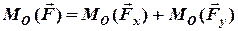 =
= 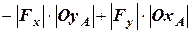 , (3.5)
, (3.5)
де у першому доданку взяли знак “–” оскільки складова 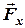 (яка має плече
(яка має плече 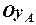 ) намагається повертати тіло відносно точки
) намагається повертати тіло відносно точки 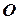 за рухом стрілки годинника та знак “+” у другому доданку, бо складова
за рухом стрілки годинника та знак “+” у другому доданку, бо складова 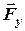 (якамає плече
(якамає плече 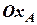 ) намагається повертати тіло відносно точки
) намагається повертати тіло відносно точки 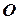 проти руху стрілки годинника.
проти руху стрілки годинника.
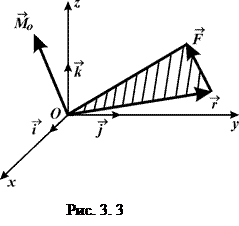 Моментом сили
Моментом сили 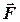 відносно осіназивається проекція на цю вісь вектора моменту сили
відносно осіназивається проекція на цю вісь вектора моменту сили 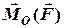 відносно точки
відносно точки 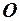 початку координат:
початку координат:
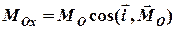 ,
,
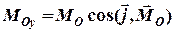 , (3.6)
, (3.6)
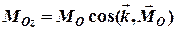
де 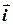 ,
, 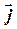 ,
, 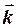 - орти осей координат (рис. 3.3). Ця фізична величина характеризує здатність сили викликати обертальний рух тіла навколо заданої осі.
- орти осей координат (рис. 3.3). Ця фізична величина характеризує здатність сили викликати обертальний рух тіла навколо заданої осі.
Аналітичні вирази для моментів сили 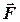 відносно декартових осей отриму-ємо як компоненти вектора
відносно декартових осей отриму-ємо як компоненти вектора 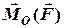
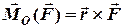 =
= 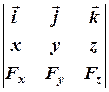 =
= 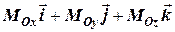 , (3.7)
, (3.7)
де 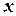 ,
,  ,
,  - декартові координати точки прикладання сили;
- декартові координати точки прикладання сили; 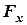 ,
, 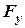 ,
, 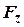 - алгебраїчні проекції сили на ці осі. Отож
- алгебраїчні проекції сили на ці осі. Отож
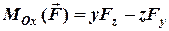 ,
,
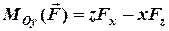 , (3.8)
, (3.8)
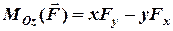 .
.
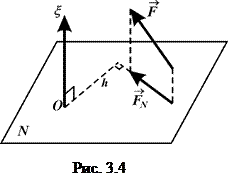 Аналізуючи формули (3.8), отримуємо ще один спосіб знаходження моменту сили відносно осі (рис. 3.4), яким користуються на практиці:
Аналізуючи формули (3.8), отримуємо ще один спосіб знаходження моменту сили відносно осі (рис. 3.4), яким користуються на практиці:
1) проводимо площину 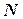 , перпендикулярну вибраній осі
, перпендикулярну вибраній осі 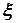 і знаходимо точку
і знаходимо точку 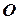 перетину цієї площини з віссю
перетину цієї площини з віссю 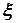 ;
;
2) визначаємо геометричну проекцію 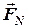 си-
си-
ли 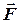 на вказану площину;
на вказану площину;
3) обчислюємо момент геометричної проекції 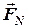 відносно точки
відносно точки 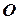 (множимо
(множимо 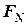 на плече
на плече 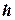 - довжину перпендикуляра, опущеного із точки
- довжину перпендикуляра, опущеного із точки 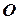 на проекцію
на проекцію 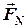 )
)
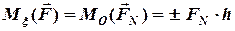 . (3.9)
. (3.9)
4) одержаному добутку приписується знак плюс, якщо із додатного напряму осі 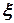 видно, що сила прагне обертати тіло навколо осі проти руху стрілки годинника, а знак мінус – коли за рухом стрілки годинника.
видно, що сила прагне обертати тіло навколо осі проти руху стрілки годинника, а знак мінус – коли за рухом стрілки годинника.
Взаємній орієнтації осі 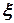 та сили
та сили 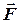 , які зображені на рис. 3.4, відповідає випадок
, які зображені на рис. 3.4, відповідає випадок 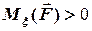 , тому
, тому 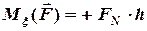 .
.
Отже, на практиці момент сили відносно осі, визначається як алгебраїчне значення добутку модуля проекції сили 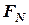 на плече
на плече 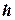 відносно точки
відносно точки 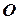 перетину осі з площиною.
перетину осі з площиною.
Момент сили відносно осі дорівнює нулю у двох випадках:
а) коли 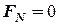 – проекція сили на площину, яка перпендикулярна осі, дорівнює нулю, тобто коли сила
– проекція сили на площину, яка перпендикулярна осі, дорівнює нулю, тобто коли сила 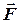 і вісь
і вісь 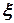 паралельні;
паралельні;
б) коли 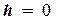 – плече проекції дорівнює нулю, тобто коли проекція сили
– плече проекції дорівнює нулю, тобто коли проекція сили 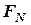 проходить через точку
проходить через точку 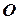 , а це означає, що лінія дії сили
, а це означає, що лінія дії сили 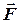 перетинає вісь.
перетинає вісь.
Контрольні запитання
1. Що називається моментом сили відносно точки? Що він характеризує? В яких одиницях вимірюється момент сили?
2. Як змінюється момент сили відносно точки, якщо точка прикладання сили зміщується вздовж лінії її дії?
3. Як визначається напрям моменту сили відносно точки?
4. Вкажіть методи обчислення модуля вектора моменту сили відносно точки.
5. Як знайти алгебраїчне значення моменту сили відносно точки? У яких випадках момент сили відносно точки дорівнює нулю?
6. Що називається моментом сили відносно осі?
7. Вкажіть методи обчислення вектора моменту сили відносно осі.
8. Як знайти алгебраїчне значення моменту сили відносно осі?
9. У яких випадках момент сили відносно осі дорівнює нулю?
10. Як змінюється момент сили відносно осі, якщо точка прикладання сили зміщується вздовж лінії її дії?
 §4. Рівняння рівноваги системи сил
§4. Рівняння рівноваги системи сил
З’ясуємо, що зміниться в системі, якщо силу перенести паралельно в іншу точку тіла. Нехай задана сила 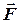 діє на тверде тіло в точці
діє на тверде тіло в точці  . В довільній точці
. В довільній точці  цього тіла прикладемо дві взаємно зрівноважені сили
цього тіла прикладемо дві взаємно зрівноважені сили 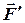 та
та 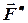 , модулі яких задовольняють умові
, модулі яких задовольняють умові 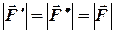 , а лінія їх дії паралельна силі
, а лінія їх дії паралельна силі 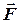 (рис.4.1).
(рис.4.1).
Отже, не змінюючи статичного стану системи, силу 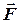 , прикладену до твердого тіла, можна перенести з точки її прикладення
, прикладену до твердого тіла, можна перенести з точки її прикладення  в будь-яку точку
в будь-яку точку  паралельно самій собі, додаючи при цьому приєднану пару сил з моментом
паралельно самій собі, додаючи при цьому приєднану пару сил з моментом
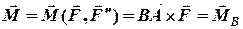 ,(4.1)
,(4.1)
який дорівнює моменту цієї сили відносно точки  . Цей метод був запропонований Пуансота носить його ім’я.
. Цей метод був запропонований Пуансота носить його ім’я.
Метод Пуансо дозволяє звестидовільну систему сил (рис.4.2) до:
1. складання сил в точці 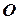
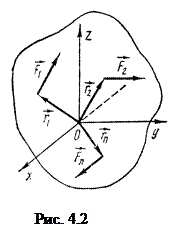
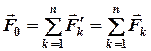 (4.2)
(4.2)
в результаті чого отримуємо головний вектор 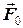 ;
;
2. геометричної суми усіх моментів сил системи відносно тієї ж точки 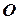
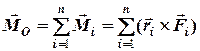 , (4.3)
, (4.3)
в результаті чого отримуємо головний момент 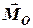 ,
,
де 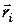 - радіус-вектор проведений точки
- радіус-вектор проведений точки 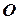 в точку прикладення сил
в точку прикладення сил 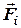 (рис.4.2).
(рис.4.2).
Можна довести, що для того, щобсистема сил знаходилась у рівновазі, необхідно і достатньо, щоб головний вектор цієї системи та її головний моментвідносно деякого центра дорівнювали нулю, тобто
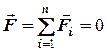 (4.4)
(4.4)
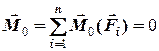 (4.5)
(4.5)
Виберемо систему координат так, щоб центр збігається з початком координат, Спроектуємо ці два векторних рівняння на координатні осі і отримаємо шість скалярних рівнянь – три для компонент сил:
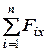 =
= 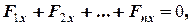 (4.6)
(4.6)
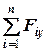 =
= 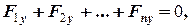 (4.7)
(4.7)
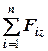 =
= 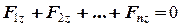 (4.8)
(4.8)
та три для проекцій моментів сил:
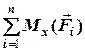 =
= 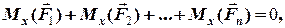 (4.9)
(4.9)
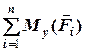 =
= 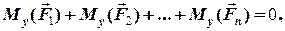 (4.10)
(4.10)
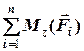 =
= 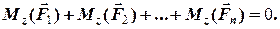 (4.11)
(4.11)
Отже, для того, щоб тіло під дією довільної системи сил знаходилось у рівновазі, необхідно і достатньо, щоб суми проекцій усіх сил на кожну із осей координат та суми моментів усіх сил відносно кожної із осей координат дорівнювали нулю, тобто виконувались шість рівнянь статики.
Розглянемо різні окремі випадки умов рівноваги для різних типів системи сил:
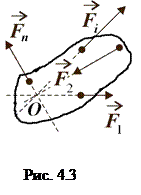 а) система збіжних сил - коли лінії дії системи сил перетинаються в одній точці (рис.3.12). Виберемо початок координат в тій точці, де сходяться сили. В цьому випадку моменти сил відносно цієї точки дорівнюють нулю, а тому три останніх рівняння системи (4.9) – (4.11) виконуються тотожньо. Для визначення умови рівноваги залишається три перших рівняння:
а) система збіжних сил - коли лінії дії системи сил перетинаються в одній точці (рис.3.12). Виберемо початок координат в тій точці, де сходяться сили. В цьому випадку моменти сил відносно цієї точки дорівнюють нулю, а тому три останніх рівняння системи (4.9) – (4.11) виконуються тотожньо. Для визначення умови рівноваги залишається три перших рівняння:
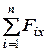 =
= 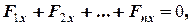
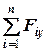 =
= 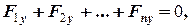 (4.12)
(4.12)
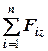 =
= 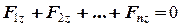 ,
,
тобто, сума проекцій всіх сил на кожну з осей координат дорівнювала нулю.
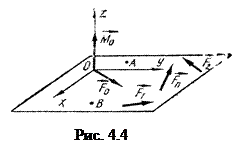 б) плоска система довільно розташованих сил –в цьому випадку всі сили лежать в одній площині (рис.4.4). Виберемо осі координат
б) плоска система довільно розташованих сил –в цьому випадку всі сили лежать в одній площині (рис.4.4). Виберемо осі координат 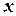 та
та  в площині сил. В цьому випадку, з 6-ти рівнянь рівноваги третє, четверте та п’яте виконуються тотожньо, тому залишається три рівняння:
в площині сил. В цьому випадку, з 6-ти рівнянь рівноваги третє, четверте та п’яте виконуються тотожньо, тому залишається три рівняння:
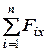 =
= 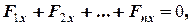
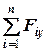 =
= 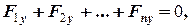 (4.13)
(4.13)
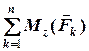 =
= 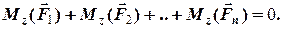
тобто, два рівняння проекцій на осі, які лежать в площині сил, та одне рівняння моментів сил відносно осі, яка перпендикулярна площині сил.
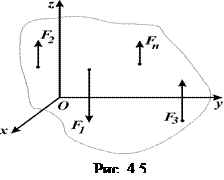 в) просторова система паралельних сил – в цьому випадку маємо систему сил, які направлені в різні боки, але паралельні між собою (рис.4.5). Виберемо вісь
в) просторова система паралельних сил – в цьому випадку маємо систему сил, які направлені в різні боки, але паралельні між собою (рис.4.5). Виберемо вісь  паралельно цим силам, тоді з 6-ти рівнянь статики два перших та останнє виконуються тотожньо, а залишаються три рівняння рівноваги:
паралельно цим силам, тоді з 6-ти рівнянь статики два перших та останнє виконуються тотожньо, а залишаються три рівняння рівноваги:
 =
=  ,
,
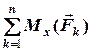 =
= 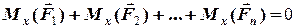 , (4.14)
, (4.14)
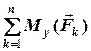 =
= 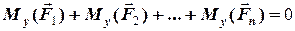 ,
,
тобто, рівняність проекцій сил на вісь, що паралельна силам, та два рівняння моментів відносно осей, які перпендикулярних цим силам.
Контрольні запитання
1. Сформулюйте теорему про паралельне перенесення сили (теорему Пуансо).
2. Чим замінюється просторова система сил при приведенні її до заданого центру?
3. Що називається головним вектором системи сил?
4. Що називається головним моментом системи сил?
5. Запишіть необхідні та достатні умови рівноваги довільної просторової системи сил.
6. Запишіть рівняння рівноваги для:
· просторової системи паралельних сил;
· збіжної системи просторових сил;
· плоскої системи сил.
Центр ваги тіла
Центром ваги твердого тіла називається точка, до якої прикладена рівнодіюча сила однорідного поля тяжіння. Ця точка не обов’язково знаходиться в тілі, наприклад, для кільця центр ваги розташований за межами твердого тіла. Визначення центра ваги тіла є важливою задачею при проектуванні та експлуатації суден, оскільки взаємне положення центра ваги судна та його метацентру визначає остійність судна.
Якщо тіло однорідне (маса рівномірно розподілена по його об’єму) та має вісь (площину або точку) симетрії, то центр ваги знаходиться на цій осі (площині або в цій точці). Якщо тіло несиметричне, або неоднорідне, то його розбивають на сукупність 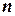 елементів, для яких координати центра ваги можна легко встановити, а центр ваги тіла знаходять за наступними формулами:
елементів, для яких координати центра ваги можна легко встановити, а центр ваги тіла знаходять за наступними формулами:
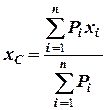 ,
, 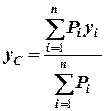 ,
, 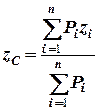 . (5.1)
. (5.1)
тут: 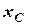 ,
, 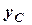 ,
, 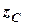 - координати центра ваги тіла,
- координати центра ваги тіла, 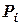 - вага елемента,
- вага елемента, 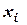 ,
, 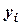 ,
, 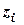 - координати центра ваги
- координати центра ваги 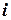 - того елемента.
- того елемента.
Зауважимо, що коли тіло має вирізи, то його вага 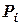 входить у розрахунки за формулою (5.1) зі знаком „–”.
входить у розрахунки за формулою (5.1) зі знаком „–”.
Для однорідних тіл формули (5.1) можуть бути спрощені. Для однорідного трьохмірного тіла з питомою вагою 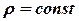 ,
, 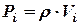 , тому в формулах (9.1) замість ваги елемента
, тому в формулах (9.1) замість ваги елемента 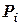 можна підставляти його об’єм
можна підставляти його об’єм 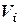 . Для двомірного (плоского) тіла з поверхневою вагою
. Для двомірного (плоского) тіла з поверхневою вагою 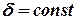 ,
, 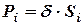 , тому замість
, тому замість 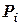 можна користуватися площею елемента
можна користуватися площею елемента 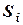 . Для лінійних однорідних тіл замість ваги елемента можна користуватися його довжиною
. Для лінійних однорідних тіл замість ваги елемента можна користуватися його довжиною 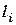 .
.
Нагадаємо формули, які визначають положення центра ваги однорідних тіл, що мають правильну форму:
1) центр ваги однорідного стрижня довжиною 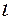 з координатами кінців (
з координатами кінців ( 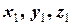 ) та (
) та ( 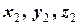 ) знаходиться на його середині, тому:
) знаходиться на його середині, тому:
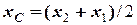 ,
, 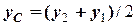 ,
, 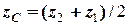 , (5.2)
, (5.2)
2) центр ваги однорідноїдуги радіуса 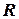 та кутом при вершині
та кутом при вершині 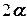 – на бісектрисі кута
– на бісектрисі кута 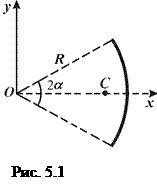 при вершині (рис. 5.1) на відстані ОС від центру дуги:
при вершині (рис. 5.1) на відстані ОС від центру дуги:
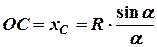 ,
, 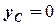 , (5.3)
, (5.3)
де кут 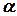 вимірюється у радіанах;
вимірюється у радіанах;
3) центр ваги однорідного паралелограма з координатами вершин ( 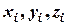 ) – в точці перетину діагоналей:
) – в точці перетину діагоналей:
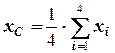 ,
, 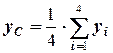 ,
, 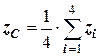 , (5.4)
, (5.4)
4) центр ваги однорідного трикутника, вершини якого мають координати (  ), – в точці перетину медіан, де вони діляться у відношенні 1:2, тому координати центру ваги трикутника знаходимо за формулами:
), – в точці перетину медіан, де вони діляться у відношенні 1:2, тому координати центру ваги трикутника знаходимо за формулами:
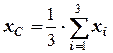 ,
, 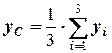 ,
, 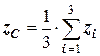 , (5.5)
, (5.5)
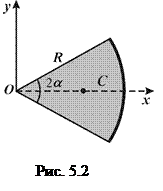
5) центр ваги однорідного сектора радіусом 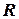 та кутом при вершині
та кутом при вершині 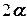 – на бісектрисі кута при вершині (рис. 5.2):
– на бісектрисі кута при вершині (рис. 5.2):
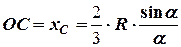 ,
, 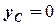 , (5.6)
, (5.6)
де вісь 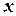 - бісектриса кута при вершині, а кут
- бісектриса кута при вершині, а кут 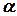 вимірюється у радіанах;
вимірюється у радіанах;
Контрольні запитання
1. Що таке центр ваги тіла? Як його знайти?
2. Як використовуються методи симетрії та вирізів для визначення центра ваги однорідного тіла. Наведіть приклади.
3. Як знайти координати центра ваги однорідного стрижня, прямокутника?
4. Як знайти координати центра ваги однорідного трикутника?
5. Як знайти координати центра ваги дуги кола, сектора?
6. Як врахувати вирізи при розрахунку центра ваги тіла?
Дата добавления: 2015-12-10; просмотров: 7664;
