РОЗДІЛ ІІ. КІНЕМАТИКА
Кінематика вивчає переміщення тіл в просторі з плином часу без з’ясування причин, які викликають рух. В кінематиці рух тіл вивчається з чисто геометричної точки зору. Якщо в задачі кінематики можна знехтувати розмірами та формою тіла, то тіло замінюють точкою. Траєкторією називається лінія, яку описує точка в процесі руху. До основних кінематичних характеристик відносяться: траєкторія, координати (положення), швидкість та прискорення точки і кутова швидкість та кутове прискорення твердого тіла.
Швидкість точки
Рух точки може бути заданий різними способами:
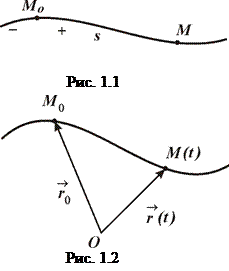 1) натуральний - цим способом зручно користуватись коли відома траєкторія руху точки. Положення рухомої точки
1) натуральний - цим способом зручно користуватись коли відома траєкторія руху точки. Положення рухомої точки  в момент часу
в момент часу 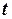 визначається дугової координати
визначається дугової координати  і законом руху
і законом руху
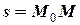
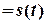 , (1.1)
, (1.1)
де  початок відліку (точку – рис. 1.1) та відомий додатній напрям відліку.
початок відліку (точку – рис. 1.1) та відомий додатній напрям відліку.
2) векторний – коли положення точки в просторі визначається радіус-вектором  , проведеним з деякого нерухомого центра
, проведеним з деякого нерухомого центра 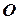 до даної точки
до даної точки  (рис. 1.2). Під час руху точки її радіус-вектор
(рис. 1.2). Під час руху точки її радіус-вектор 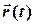 змінює свій модуль і напрям
змінює свій модуль і напрям

 . (1.2)
. (1.2)
3) координатний- полягає в тому, що положення точки задається набором координат. При розгляді руху в прямокутній декартовій системі координат (рис.1.3) вказаний спосіб зводиться до задання трьох координат 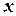 ,
,  ,
,  точки
точки 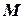 як відомих функцій часу:
як відомих функцій часу:
 ,
,  ,
, 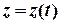 . (1.3)
. (1.3)
Зв'язок векторного метода з декартовими координатами наступний
 . (1.4)
. (1.4)
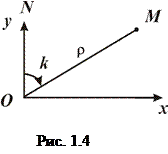 4) в навігації, в основному, користуються цилін-дричною системою координат
4) в навігації, в основному, користуються цилін-дричною системою координат 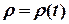 ,
,  ,
, 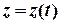 рис.1.3 на площині (полярною, координати ), але дещо зміненою. Замість азимута
рис.1.3 на площині (полярною, координати ), але дещо зміненою. Замість азимута 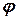 використовують курс
використовують курс 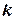 (рис. 1.4), який вимірюють від „норду” (напряму на північ) і відлік кута ведуть за напрямом руху стрілки годинника. Якщо вісь
(рис. 1.4), який вимірюють від „норду” (напряму на північ) і відлік кута ведуть за напрямом руху стрілки годинника. Якщо вісь  сумістити з „нордом”, а вісь
сумістити з „нордом”, а вісь 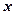 снрямувати горизонтально, то отримаємо зв’язок між координатами декартової та навігаційної систем:
снрямувати горизонтально, то отримаємо зв’язок між координатами декартової та навігаційної систем:
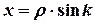 ,
,  . (1.5)
. (1.5)
 Швидкістю точки в момент часу
Швидкістю точки в момент часу  називається величина, яка характеризує зміну вектора
називається величина, яка характеризує зміну вектора 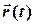 з плином часу (рис. 1.5)
з плином часу (рис. 1.5)
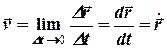 . (1.6)
. (1.6)
Вектор швидкості точки в даний момент часу дорівнює першій похідній від радіус-вектора по часу і напрямлений по дотичній до траєкторії у відповідній точці у бік руху (рис. 1.5).
Коли рівняння руху точки задано в декартових координатах, то
 . (1.7)
. (1.7)
Отже, алгебраїчні проекції вектора швидкості на кожну з осей (рис. 1.6) дорівнюють похідним по часу від відповідної координати точки, яка рухається
 ,
,  ,
,  . (1.8)
. (1.8)
Модуль вектора швидкості обчислюють за формулою
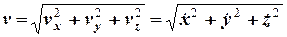 . (1.9)
. (1.9)
 Коли рівняння руху точки задано натуральним способом (рис. 1.6), то дугова координата є функцією часу, то радіус-вектор
Коли рівняння руху точки задано натуральним способом (рис. 1.6), то дугова координата є функцією часу, то радіус-вектор 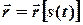 , тоді
, тоді
 , (1.10)
, (1.10)
де
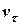 =
= 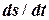 (1.11)
(1.11)
- алгебраїчне значення миттєвої швидкості, а  - одиничний вектор (орт), який направлений по дотичній до кривої в сторону зростання дугової координати (рис. 1.6, а, б) і не залежить від напряму руху точки.
- одиничний вектор (орт), який направлений по дотичній до кривої в сторону зростання дугової координати (рис. 1.6, а, б) і не залежить від напряму руху точки.
Якщо  , то точка рухається в напрямі зростання дугової координати і напрям швидкості
, то точка рухається в напрямі зростання дугової координати і напрям швидкості  співпадає з напрямом орта
співпадає з напрямом орта 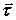 (рис. 1.6, а). При
(рис. 1.6, а). При 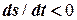 точка рухається в напрямі зменшення дугової координати і вектор швидкості
точка рухається в напрямі зменшення дугової координати і вектор швидкості  протилежний до напряму орта
протилежний до напряму орта 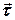 (рис. 1.6, б).
(рис. 1.6, б).
Контрольні запитання
1. Що вивчає кінематика?
2. В яких випадках тіло можна вважати точкою?
3. Що таке траєкторія руху точки? Які типи траєкторій вам відомі?
4. Які величини потрібно знати, щоб задати закон руху точки для векторного способу, координатного та природного способів описання?
5. Як знайти напрям та величину вектора миттєвої швидкості?
6. Як знайти компоненти вектора швидкості та його модуль у декартовій системі координат?
Прискорення точки
Прискорення характеризує зміну швидкості з плином часу. Миттєве прискорення точки в даний момент часу визначається першою похідною по часу від вектора швидкості, або другою похідною по часу від радіус-вектора точки
 . (2.1)
. (2.1)
Вектор прискорення напрямлений по зміні вектора швидкості 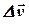 .
.
Коли рівняння руху точки задано в декартових координатах, то з формули (1.8), взявши похідну, отримуємо
 =
=  , (2.2)
, (2.2)
де 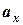 ,
,  ,
,  - алгебраїчні проекції прискорення на декартові осі координат, які дорівнюють другим похідним по часу від відповідних координат точки або першим похідним по часу від проекцій швидкості на відповідні осі. Модуль вектора прискорення визначається за формулою
- алгебраїчні проекції прискорення на декартові осі координат, які дорівнюють другим похідним по часу від відповідних координат точки або першим похідним по часу від проекцій швидкості на відповідні осі. Модуль вектора прискорення визначається за формулою
 . (2.3)
. (2.3)
У випадку натурального способу вектор швидкості  , тому для вектора прискорення отримуємо
, тому для вектора прискорення отримуємо
 . (2.6)
. (2.6)
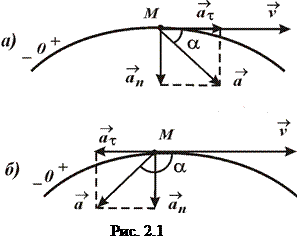 Отже, повне прискорення скла-дається з двох взаємно перпендикулярних складових:
Отже, повне прискорення скла-дається з двох взаємно перпендикулярних складових:
1) тангенціального прискорення 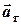 , яке напрямлене вздовж дотичної до траєкторії і характеризує зміну швидкості за модулем
, яке напрямлене вздовж дотичної до траєкторії і характеризує зміну швидкості за модулем
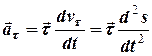 . (2.7)
. (2.7)
Якщо алгебраїчне значення швидкості зростає (  , рис. 2.1, а), то напрями
, рис. 2.1, а), то напрями 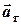 і
і 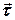 співпадають, а коли алгебраїчне значення швидкості зменшується, (
співпадають, а коли алгебраїчне значення швидкості зменшується, (  , рис. 2.1, б) – напрями векторів
, рис. 2.1, б) – напрями векторів 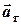 і
і 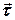 протилежні;
протилежні;
2) нормального прискорення, яке характеризує зміну швидкості за напрямом
 , (2.8)
, (2.8)
де 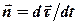 - орт, який перпендикулярний до вектора швидкості і направлений у той бік, куди повертається вектор швидкості (до центру дуги, по якій рухається точка),
- орт, який перпендикулярний до вектора швидкості і направлений у той бік, куди повертається вектор швидкості (до центру дуги, по якій рухається точка), 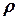 - радіус кривизни траєкторії.
- радіус кривизни траєкторії.
Вектор повного прискорення направлений по діагоналі прямокутника, побудованого на векторах 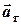 та
та  (рис. 2.1), а його модуль
(рис. 2.1), а його модуль
 . (2.9)
. (2.9)
Тангенціальне прискорення, яке є проекцією повного прискорення на вектор швидкості (рис. 2.1) можна визначити через скалярний добуток
 =
=  =
=  .
.
З останнього рівняння отримуємо формулу для обчислення тангенціального прискорення через компоненти векторів швидкості та прискорення:
 =
= 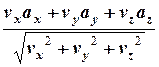 . (2.10)
. (2.10)
Якщо відомі величини повного 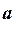 та тангенціального
та тангенціального  прискорень, то можна визначити нормальне прискорення точки
прискорень, то можна визначити нормальне прискорення точки
 =
= 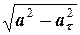 =
=  , (2.11)
, (2.11)
та знайти радіус кривизни траєкторії
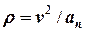 . (2.12)
. (2.12)
Розглянемо окремі випадки руху точки:
коли 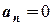 точка рухається прямолінійно (
точка рухається прямолінійно ( 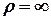 ), або у випадку криво-лінійного руху, в той момент часу, коли миттєве значення швидкості
), або у випадку криво-лінійного руху, в той момент часу, коли миттєве значення швидкості  ; в цих випадках прискорення має лише тангенціальну складову, а вектор прискорення напрямлений до дотичній до траєкторії;
; в цих випадках прискорення має лише тангенціальну складову, а вектор прискорення напрямлений до дотичній до траєкторії;
коли  величина швидкості стала, в цьому випадку прискорення має лише нормальну складову, а вектор прискорення напрямлений до центру кривизни траєкторії.
величина швидкості стала, в цьому випадку прискорення має лише нормальну складову, а вектор прискорення напрямлений до центру кривизни траєкторії.
Контрольні запитання
1. Як визначається миттєве прискорення точки? Як знайти напрям вектора миттєвого прискорення?
2. Як знайти компоненти вектора прискорення та його модуль в декартовій системі координат?
3. Поясніть роль тангенціального прискорення у зміні швидкості.
4. Як знайти тангенціальне прискорення через компоненти швидкості та прискорення в декартовій системі координат?
5. Поясніть роль нормального прискорення у зміні швидкості.
6. Як знайти модуль повного прискорення, якщо відомі його тангенціальна та нормальна складові?
7. Для якого руху точки по криволінійній траєкторії кут між векторами швидкості та прискорення: а) гострий? б) тупий? в) прямий?
Дата добавления: 2015-12-10; просмотров: 1022;
