В’язі та їхні реакції
РОЗДІЛ I. СТАТИКА
Статика є розділ теоретичної механіки, який вивчає:
– властивості сил, прикладених до твердого тіла;
– приведення складних систем сил до більш простих;
– умови рівноваги тіл під дією сил.
Основна задача статикиє знаходження тих умов, коли механічна система знаходиться в рівновазі.
Нагадаємо, що в теоретичній механіці тіла вважаються абсолютно твердими – тобто такими, що віддаль між довільними точками яких залишається незмінною. Тверде тіло, на переміщення якого не накладено жодних обмежень, називається вільним. Якщо на рух твердого тіла накладені обмеження, то тіло називається невільним, а тіла, які обмежують рух такого тіла, називаються в’язями.
Аксіоми статики
Аксіоми статики встановлені експериментально та формулюють закони, яким задовольняють сили, що діють на тіла. Опираючись на них можна отримати всі закони статики.
Аксіома 1 (про складання сил). Дві сили  та
та 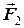 прикладені в одній точці
прикладені в одній точці  , можна замінити рівнодійною
, можна замінити рівнодійною
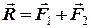 , (1.1)
, (1.1)
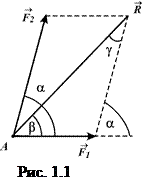 яку знаходимо геометрично (рис.1.1) за правилом паралелограма, побудованого на цих силах як на сторонах, або за правилом трикутника.
яку знаходимо геометрично (рис.1.1) за правилом паралелограма, побудованого на цих силах як на сторонах, або за правилом трикутника.
Для знаходження модуля рівнодійної скористаємося теоремою косинусів:
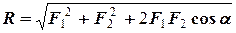 , (1.2)
, (1.2)
де 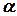 – кут між силами
– кут між силами  та
та 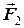 , а напрям сили
, а напрям сили  (кут
(кут 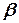 , який вона утворює з силою
, який вона утворює з силою  , або кут
, або кут 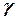 , який вона утворює з силою
, який вона утворює з силою 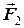 ), знаходимо за теоремою синусів (рис. 1.1):
), знаходимо за теоремою синусів (рис. 1.1):
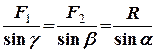 . (1.3)
. (1.3)
 Аналогічно, одну силу
Аналогічно, одну силу  можна розкласти на складові
можна розкласти на складові  та
та 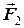 , якщо відомі (або обрані) напрями, вздовж яких діють складові. Якщо для сили
, якщо відомі (або обрані) напрями, вздовж яких діють складові. Якщо для сили  задані напрями
задані напрями 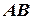 та
та  (кут між ними
(кут між ними 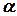 та кут
та кут 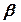 (або
(або 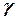 ), який утворює одна їз складових з вектором
), який утворює одна їз складових з вектором 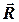 ), то через початок вектора
), то через початок вектора  креслимо напрями
креслимо напрями 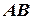 та
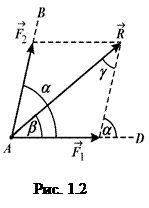
та  , а через кінець цього вектора проводимо прямі, їм паралельні (рис. 1.2) і отримуємо складові сили
, а через кінець цього вектора проводимо прямі, їм паралельні (рис. 1.2) і отримуємо складові сили  та
та 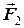 . Модулі складових
. Модулі складових  та
та 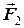 сили
сили  знаходимо за теоремою синусів - формула (1.3).
знаходимо за теоремою синусів - формула (1.3).
Аксіома 2 (про взаємно зрівноважені сили). Якщо дві сили, які прикладені до твердого тіла в одній точці, направлені в протилежні напрями та мають рівні модулі, то вони взаємно зрівноважуються. З формули (1.1) за умови 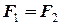 та
та  знаходимо, що
знаходимо, що 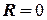 . Такі сили називаються взаємно зрівноважені і не можуть викликати дію на точку, бо дія одної врівноважується іншою.
. Такі сили називаються взаємно зрівноважені і не можуть викликати дію на точку, бо дія одної врівноважується іншою.
Аксіома 3 (про векторний нуль). Дія системи сил на тверде тіло не зміниться, якщо до неї приєднати або від’єднати систему взаємно зрівноважених сил (векторний нуль). Таким чином, всяка система сил, що діє на тверде тіло, і така, яка отримана з даної шляхом приєднання або від’єднання зрівноваженої системи сил, чинить на тіло однакову дію.
 Як наслідок з даної аксіоми отримуємо, що в статиці твердого тіла сила є ковзний вектор. Дійсно, нехай до твердого тіла прикладена сила
Як наслідок з даної аксіоми отримуємо, що в статиці твердого тіла сила є ковзний вектор. Дійсно, нехай до твердого тіла прикладена сила 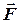 в точці
в точці  (рис.1.3). Прикладемо в точці
(рис.1.3). Прикладемо в точці  , що знаходиться на лінії дії цієї сили, дві сили
, що знаходиться на лінії дії цієї сили, дві сили  та
та 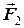 рівні за модулем силі
рівні за модулем силі 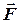 та направлені по цій лінії в протилежні сторони. Тепер відкинемо сили
та направлені по цій лінії в протилежні сторони. Тепер відкинемо сили 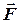 та
та 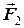 , як взаємно зрівноважені. Тоді до тіла буде прикладена сила
, як взаємно зрівноважені. Тоді до тіла буде прикладена сила  =
= 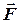 , але тепер в точці
, але тепер в точці  , яка еквівалентна силі
, яка еквівалентна силі 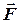 в точці
в точці  .
.
Аксіома 4 (накладання та звільнення від в’язей). Рівновага тіла не порушиться, якщо на нього накласти додаткові в’язі (після того, як рівновага установиться), або відкинути в’язі і замінити їх реакціями, які прикладені до даного тіла (системи тіл).
Аксіома 5 (принцип отвердіння).Якщо внаслідок вчиненої деформації настала рівновага тіла, яке деформується, то ця рівновага не порушиться від подальшого отвердіння тіла (якщо тіло стане абсолютно твердим). Оскільки тут йде мова не про фізичне отвердіння, то отвердіння можна розглядати як накладення жорстких в’язей між частинками тіла.
Внаслідок принципу отвердіння усі висновки статики абсолютно твердого тіла застосовуються до реальних деформованих тіл.
Контрольні запитання
1. Що вивчає статика?
2. У чому полягає основна задача статики?
3. Дайте визначення абсолютно твердого тіла?
4. Сформулюйте основні аксіоми статики.
5. Сформулюйте властивості сили як ковзного вектора.
6. Яку силу називають рівнодійною? Вкажіть правила її знаходження.
7. Які дві системи сил називаються зрівноваженими?
В’язі та їхні реакції
Нагадаємо, що в’язяминазиваютьсятіла, які обмежують переміщення невільного тіла. Реакцією в’язі називається сила, з якою в’язь діє на точку або тверде тіло. Величини цих реакцій можуть бути знайдені з умов рівноваги, оскільки вони залежать від активних сил, що діють на механічну систему. Розглянемо найпростіші в’язі.
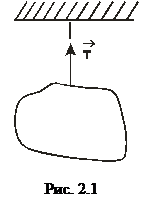 1. Нитка (трос, мотузка, ланцюг). Вважається, що нитка невагома, гнучка та нерозтяжна. Якщо до кінця нитки закріпити вантаж вагою
1. Нитка (трос, мотузка, ланцюг). Вважається, що нитка невагома, гнучка та нерозтяжна. Якщо до кінця нитки закріпити вантаж вагою 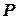 , то дослідні дані підтверджують, що реакція нитки
, то дослідні дані підтверджують, що реакція нитки 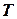 (рис.2.1) спрямована вздовж неї до точки закріплення, прикладена до тіла та за модулем дорівнює вазі вантажу
(рис.2.1) спрямована вздовж неї до точки закріплення, прикладена до тіла та за модулем дорівнює вазі вантажу 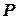 .
.
 2. Стрижень. Стрижень припускається прямолінійним, невагомим та з шарнірами на кінцях. На відміну від нитки (рис.2.1) , стрижень у рівновазі може бути як розтягнутим, так і стиснутим. Реакція стрижня спрямована завжди вздовж нього. Якщо стрижень розтягнутий, то реакція спрямована у середину, якщо стрижень стиснутий - то назовні.
2. Стрижень. Стрижень припускається прямолінійним, невагомим та з шарнірами на кінцях. На відміну від нитки (рис.2.1) , стрижень у рівновазі може бути як розтягнутим, так і стиснутим. Реакція стрижня спрямована завжди вздовж нього. Якщо стрижень розтягнутий, то реакція спрямована у середину, якщо стрижень стиснутий - то назовні.
3.В’язі можуть бути у вигляді нерухомих шарнірів циліндричних (з нерухомою віссю обертання (рис.2.2,а)) – реакція в’язі  розміщена в площині перпендикулярній осі обертання та має дві невідомі величини
розміщена в площині перпендикулярній осі обертання та має дві невідомі величини  та
та 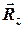 , та сферичних (з нерухомим центром обертання (рис.2.2,б) – реакція в’язі
, та сферичних (з нерухомим центром обертання (рис.2.2,б) – реакція в’язі  визначається трьома проекціями
визначається трьома проекціями 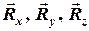 на три осі координат.
на три осі координат.
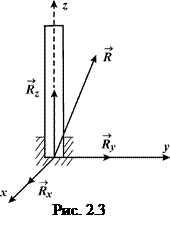 4Трьома складовими визначається також реакція підп’ятника (упорного підшипника) (рис. 2.3), який є циліндричним шарніром з опорною площиною
4Трьома складовими визначається також реакція підп’ятника (упорного підшипника) (рис. 2.3), який є циліндричним шарніром з опорною площиною  . Тому крім зазначених двох реакцій
. Тому крім зазначених двох реакцій 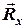 та
та  , як у випадку циліндричного шарніра, виникає ще перпендикулярна складова
, як у випадку циліндричного шарніра, виникає ще перпендикулярна складова 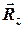 вздовж осі
вздовж осі  .
.
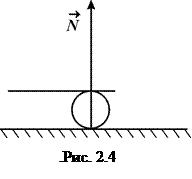 5В’язь може здійсню-ватись уформікотків, тоді виникає шарнірно рухома опора. Якщо нехтувати тертям котків, то лінія дії реакції такої опори (рис.2.4) спрямована по нормалі до опорної площини котків.
5В’язь може здійсню-ватись уформікотків, тоді виникає шарнірно рухома опора. Якщо нехтувати тертям котків, то лінія дії реакції такої опори (рис.2.4) спрямована по нормалі до опорної площини котків.
Контрольні запитання
1. Що називається в’язью?
2. В чому полягає принцип звільнення від в’язів?
3. Перерахуйте основні типи в’язів, для яких напрями дії реакцій відомі?
4. Вкажіть в’язі, які мають одну реакцію? Дві реакції? Три реакції?
Дата добавления: 2015-12-10; просмотров: 3917;
