Методы расчета надежности оператора

Как уже указывалось, основным видом отказов человека-оператора являются ошибки. Все ошибки оператора разделяются на закономерные и случайные. Примерами закономерных ошибок могут быть следующие. В системе применено кодирование цветом. Естественно, что оператор-дальтоник при поиске нужного сигнала будет допускать ошибку, хотя все остальные операции может выполнять правильно. В другом случае оператору нужно вычислять значение логарифма от какого-то показания прибора. Оператор не знает, как правильно вычислять логарифм, и поэтому при вычислении допускает ошибку. Характерным в этих примерах является профессиональная непригодность или неподготовленность оператора к определенному виду деятельности. При правильной организации труда операторов закономерных ошибок не бывает.

Случайные ошибки операторов характеризуются тем, что при каждом опыте мы не можем однозначно указать, будет ошибка или нет, мы можем только определить вероятность возникновения этих ошибок. Конечно, это не означает беспричинность ошибок, просто на данном этапе развития психологии мы не можем заранее определить и указать эти причины.

Для проведения расчетов надежности оператора необходимо провести классификацию ошибок, руководствуясь при этом следующими положениями. Во-первых, предлагаемая классификация должна вскрывать психологическую сущность ошибок. Во-вторых, она должна в то же время классифицировать ошибки по степени влияния их на результат выполнения задачи СЧМ. Эта классификация ошибок приведена на рис. 44.

Все случайные ошибки делятся на прогнозируемые и непрогнозируемые. Это деление обусловлено тем, что даже в самых идеальных условиях работы операторы допускают 1—2% ошибочных действий. Причины этих ошибок совершенно не выявлены и обусловлены колебаниями на молекулярном уровне. Такие ошибки называются непрогнозируемыми. При изменении условий работы (информационная перегрузка, недостаток времени, повышенный уровень шумов или температуры и т. д.) число ошибок возрастает. Хотя эти ошибки также являются случайными, т. е. при каждом испытании мы заранее не можем указать исход этого испытания, однако мы можем указать общее число ошибок, вызванных действием данного фактора. Иными словами, на основании известных закономерностей операторской деятельности мы можем оценить ожидаемое значение вероятности безошибочной работы при наличии данного фактора. Поэтому такие ошибки относятся к числу прогнозируемых.

Как прогнозируемые, так и непрогнозируемые ошибки по степени влияния на конечный результат могут быть трех типов. Ошибки первого типа своевременно исправляет сам оператор и они никакого влияния на результат решения не оказывают. Такие ошибки называются сбоями. Ошибки второго типа оператор также исправляет, но несвоевременно. Такие ошибки будем

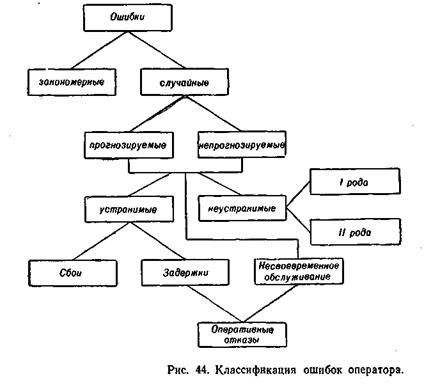
называть задержками. Сбои и задержки принадлежат к числу устранимых ошибок. Ошибки третьего типа оператор вообще не устраняет, их называют неустранимыми, или существенными. Эти ошибки могут быть двух родов: невыполнение (пропуск) нужного действия и неправильные действия. По аналогии с теорией статистических решений эти ошибки называются соответственно ошибками первого и второго рода.

Кроме рассмотренных ошибок, задача может быть не выполнена и при правильных действиях, на выполнение которых тратится время, превышающее некоторый лимит. Совместно с задержками ошибки подобного рода называются оперативными отказами [50].

Вероятность безошибочного выполнения отдельной операции

ф (10.23)

где р₀ — вероятность того, что при выполнении операции не будет допущено никаких ошибок;

р_и— условная вероятность исправления допущенной ошибки;

р_и(τ) — условная вероятность исправления допущенной ошибки за время, не превышающее некоторого допустимого значения τ.

При известных вероятностях безошибочного выполнения операций, вычисляемых по формуле (10.23), может быть определена вероятность безошибочного выполнения оператором всей задачи. Для этого должна быть задана структура деятельности оператора в виде последовательности отдельных операций. Такие методы расчета надежности носят название структурных. Рассмотрим один из них.

В течение фазы устойчивой работоспособности оператора (фаза II, рис. 43, б) и предположении о простейшем (пуассоновском) характере потока ошибок вероятность отсутствия ошибок при выполнении k операций j-го вида в соответствии с (10. 5) равна:

ф (X.24)

где λ_j— интенсивность ошибок i-го вида, вычисляемая согласно выражению (10.18).

Если задача состоит из r различных видов операций, а общее число операций j-го вида (j = 1, 2, .. ., r) равно k_j , то вероятности безошибочного выполнения всех k_j операций различных видов определяются по формулам:

ф(10.25)

Если считать ошибки независимыми и не влияющими друг на друга, вероятность безошибочного выполнения всего комплекса операций, входящих в задачу, равна:

ф(10.26)

В этом выражении вероятности безошибочного выполнения отдельных операций p_j вычисляют по формуле (10.18) или находят статистически по результатам эксперимента.

Полученное выражение справедливо лишь для участка II кривой, изображенной на рис. 43, б. В общем случае нужно пользоваться выражением

ф (10.27)

Порядок расчета надежности оператора покажем на следующем примере. При возникновении аварии в технологическом процессе на пульте оператора (рис. 45) включается звуковой сигнал. По этому сигналу оператор должен оценить, в какой из 4-х возможных зон (А, Б, В, Г) находятся показания прибора П₁. В любом случае оператор должен перейти на ручной режим работы (включить тумблер В₁), а после этого в течение определенного времени

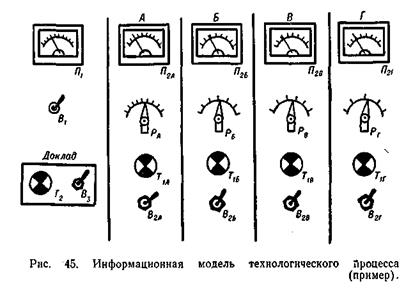
установить ручку регулировки в положение, соответствующее показанию одного из приборов П₂. При этом загорается транспарант Т₁. Затем включают дополнительный механизм (с помощью тумблера В₂), и включением тумблера В₃ следует доклад старшему диспетчеру о переходе на ручной режим. При получении им доклада загорается транспарант T_{2 .}

Определим вероятность перевода процесса на ручной режим. Общее число различных видов операций r = 5 (считывание показаний с прибора, поворот ручки, включение тумблера, восприятие загорания транспаранта, выбор одного из четырех приборов — операция «ИЛИ»). Число операций каждого вида соответственно равно: k₁ = 2, k₂ = 1, k₃ = 3, k₄ = 2, k₅ = 1.

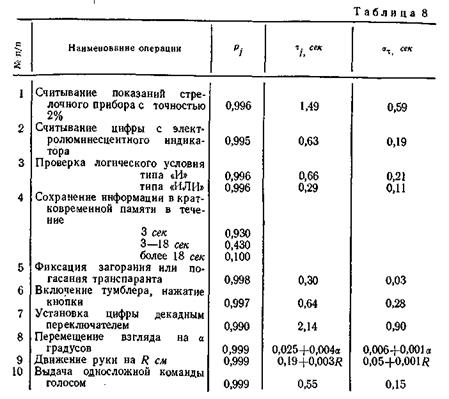
Справочные данные по надежностным и временным характеристикам отдельных операций, взятые из литературных источников, приведены в табл. 8.

При пользовании таблицей следует иметь в виду, что приведенные в ней данные носят ориентировочный характер ввиду сильной зависимости показателей деятельности оператора от различного рода факторов. На основании данных таблицы по формуле (10. 27) находим

Р_оп = 0.996² . 0,990 . 0,997^s . 0.998² . 0,996 = 0,961.