Методы оценки времени решения задач оператором
Для определения вероятности возникновения оперативного отказа необходимо знать время решения задачи оператором. На ранних этапах проектирования СЧМ нет возможности получить это время (также, как и надежность оператора) экспериментальным путем. Поэтому необходимые временные характеристики получают аналитическими методами и называют их методами прогнозирования. В основе методов прогнозирования лежит знание структуры деятельности оператора (последовательности выполняемых действий), поэтому их также относят к числу структурных методов.
Существует несколько методов прогнозирования времени решения задачи оператором: теоретико-информационный, метод моделирования, сетевой и др.
Сущность информационного метода заключается в том, что между количеством перерабатываемой оператором информации и временем, затраченным на ее переработку, существует определенная зависимость. Методы подсчета количества информации, перерабатываемой при решении ряда перцептивных и мыслительных задач, подробно рассмотрены в гл. П. В последнее время информационные методы начинают применяться и для оценки двигательных задач, ибо любая деятельность оператора немыслима без движений, на которые также затрачивается определенное время.
В качестве меры энтропии двигательной задачи используется величина [99]
ф (X.41)
где А ¾ амплитуда движения руки, т.е. расстояние, на которое перемещается рука;
W — ширина цели, т.е. ширина органа управления, на который должна попасть рука оператора.
Выражение (10.41) учитывает тот интуитивный факт, что энтропия оказывается тем больше, чем дальше оператор находится от органа управления и чем меньше размеры органа управления.
Обычно информация с точки зрения скорости ее переработки оператором может быть нескольких видов. Эти виды информации подробно рассмотрены в гл. II. Среднее время переработки всей информации при решении задачи оператором равно:
ф(10.42)
где Нi — количество информации i-го вида, перерабатываемой при решении задачи;
Vi — скорость переработки информации i-го вида.
Значения скорости переработки некоторых видов информации приводятся в табл. 9.
Таблица 9
| № | Вид информации | V, дв. ед./сек |
| Восприятие поступающих сигналов | 18,2—24,4 | |
| Решение логических задач | 8,2—15,1 | |
| Арифметические операции | 6,0—12,0 | |
| Информация, подлежащая долговременному запоминанию | 16,4—24,5 | |
| Нахождение органа управления | 18,2—24,4 | |
| Двигательные задачи | 8,5—11,5 | |
| Выдача речевых команд | 17,8—26,3 | |
| Снятие показаний со стрелочных приборов | 4,2—8,4 |
Данные табл. 9 носят ориентировочный характер, поэтому их можно использовать лишь для прикидочных расчетов времени т. В тех случаях, когда информацию не разделяют на отдельные виды, а оценивают общую энтропию
системы «вход — выход» оператора (т. е. производится укрупнение информации), величина V =2,0 ¾4,l дв. ед./сек.
Метод моделирования заключается в том, что деятельность оператора представляется в виде суммы п отдельных независимых последовательно выполняемых операций. Для каждой из этих операций предполагается известный закон распределения времени выполнения этой операции. В соответствии с заложенной в память ЭВМ программой формируется по заданному закону время выполнения первой операции t1, затем время t2 и так далее, пока не будет сформировано время выполнения п-й операции. Общее время решения задачи находят как сумму τ=t1+t2+ …… +tn . Процесс повторяется N раз, в результате чего получают N значений времени τ. По этим значениям строят закон распределения времени решения задачи и вычисляют его основные характеристики τ и στ [30].
При необходимости модель может учитывать и ошибки в выполнении элементарных операций. Для этого в память машины вводят значения рj — вероятности безошибочного выполнения j-й операции. На каждом шаге ЭВМ вычисляет время tj и по жребию в соответствии с вероятностью pj проверяет безошибочность выполнения j-и операции. Операция считается выполненной безошибочно, если соблюдено условие
Pj<ξ, (10.43)
где ξ — число, равномерно распределенное в интервале [0, 1], выработанное машиной на i-м шаге. Вполне очевидно, что вероятность выполнения условия (10.43) равна pj.
Если условие (10. 43) не выполнено, то считается, что j-я операция совершена с ошибкой. В зависимости от принятой программы работы эту операцию повторяют вновь либо повторяют все или часть предшествующих операций и т. д. Выполнение той или иной программы обусловлено характером исследуемой деятельности.
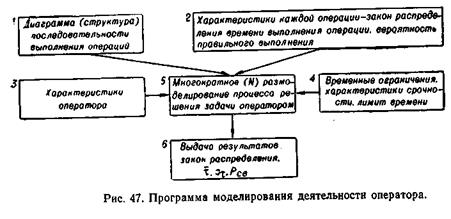
Еще более полная модель получится, если различать индивидуальные характеристики операторов, временные ограничения, налагаемые на процесс решения задачи, вводить различную срочность выполнения отдельных операций и т. д. Программа моделирования может быть представлена блок-схемой, изображенной на рис. 47.
Блоки 1, 2, 3, 4 осуществляют ввод исходных данных, блок 5 проводит собственно моделирование заданное число N раз. По результатам N реализаций блок 6 вычисляет и выдает на печать закон распределения времени выполнения задачи, его числовые характеристики τ и στ, вероятность своевременного выполнения задачи и другие величины.
Основным недостатком рассмотренных методов является использование гипотезы последовательности выполнения оператором отдельных операций. В то же время известно, что для деятельности человека характерно частичное совмещение во времени отдельных операций. Поэтому рассмотренные методы дают, как правило, завышенные значения времени выполнения работы человеком-оператором.
 Указанного недостатка можно избежать, если использовать для определения времени решения задачи оператором сетевые модели, применяемые в методах сетевого планирования и управления (СПУ). Для построения сетевой модели деятельность оператора также разбивается на элементарные операции: нажатие кнопки, включение тумблера, движение руки, перемещение взгляда, считывание показаний и т. д.
Указанного недостатка можно избежать, если использовать для определения времени решения задачи оператором сетевые модели, применяемые в методах сетевого планирования и управления (СПУ). Для построения сетевой модели деятельность оператора также разбивается на элементарные операции: нажатие кнопки, включение тумблера, движение руки, перемещение взгляда, считывание показаний и т. д.
Основными понятиями сетевой модели являются работа, событие и путь. Сетевая модель в нашем понимании есть графическое изображение процесса решения задачи оператором, показывающее взаимосвязь всех работ и событий, необходимых для достижения конечной цели.
На языке сетевых моделей элементарные операции, входящие в решаемую оператором задачу, называются работами, а моменты их завершения — событиями. Каждая работа в конечном итоге должна быть охарактеризована двумя параметрами — математическим ожиданием и дисперсией продолжительности (времени выполнения) этой работы. При построении сетевой модели может быть учтен тот факт, что отдельные перцептивные, мыслительные н двигательные процессы могут быть частично совмещены во времени. Общее время решения задачи оператором равняется продолжительности критического пути [90]:
τ = max Li, (10.44)
где Li — продолжительность i-гo полного пути, равная сумме продолжительности работ, лежащих на этом пути.
Одним из обязательных условий построения сетевой модели является независимость продолжительности выполнения отдельных работ. Гипотеза независимости была экспериментально проверена на большой группе операторов методом корреляционного анализа.
Следовательно, величина τ представляет собой сумму некоторого числа независимых случайных величин и в практике СПУ, считается подчиненной нормальному закону распределения.
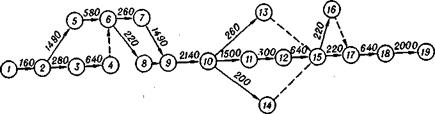
Рис. 48. Сетевая модель работы оператора.
Параметры распределения (10.45) или, что то же самое, параметры критического пути при условии независимости отдельных работ равны:
| S • |
ф(10.46)
где ¯τij, σij2 — математические ожидания и дисперсии продолжительностей критических работ.
Рассмотренная методика определения времени решения задачи оператором может быть применена на этапе проектирования СЧМ, когда проведение эксперимента невозможно из-за отсутствия реальной аппаратуры, однако известна структура деятельности оператора и типы используемых индикаторов и органов управления.
В качестве примера на рис. 48 показана сетевая модель, изображающая процесс решения оператором задачи по ликвидации аварийной ситуации с помощью информационной модели (рис. 45). Коды, наименования и продолжительность действительных работ приведены в табл. 10.
На рис. 48 введено 5 фиктивных работ. Работа 4—6 введена потому, что движение руки к ручке Р (6—8) и перемещение взгляда к П2 (6—7) возможно только после выполнения событий 4 (В1 включен) и 6 (решение о дальнейших действиях принято). Аналогичный смысл имеют остальные фиктивные работы.
Работы 10—11, 18—19 являются ожиданиями и определяются особенностями технологического процесса. Критическим путем для модели, изображенной на рис. 48, является путь 1—2, 2—5, 5—6, 6—7, 7—9, 9—10, 10—11, 11—12, 12—15, 15—17, 17—18, 18—19. На рис. 48 он отмечен жирной линией. По данным табл. 10 в соответствии с формулами (10. 46) находят параметры критического пути, которые в данном случае равны ¯τ=11,24 сек, στ=1,41 сек.
Таблица 10
| Код | Наименование работы | ¯τj, мсек | τj2, мсек2 |
| 1-2 | Латентный период звукового сигнала | 312 | |
| 2-3 | Движение руки к тумблеру B1 | 702 | |
| 3-4 | Включение тумблера B1 | 2802 | |
| 2-5 | Считывание показаний П1 | 5902 | |
| 5-6 | Принятие решений о дальнейших действиях — переработка 2 бит информации | 1902 | |
| 6-7 | Движение взгляда к П2 | 702 | |
| 6- 8 | Движение руки к Р | 502 | |
| 7-9 | Считывание показаний П2 | 5902 | |
| 9-10 | Установка Р в требуемое положение | 9002 | |
| 10-11 | Ожидание загорания Т1 | — | |
| 11-12 | Восприятие зажигания Т1 | 332 | |
| 10-13 | Перемещение взгляда на Т1, В2 | 702 | |
| 10-14 | Движение руки к тумблеру В2 | 452 | |
| 12-15 | Включение тумблера В2 | 2802 | |
| 15-16 | Перемещение взгляда на Т2, В3 | 602 | |
| 15-17 | Движение руки к В3 | 502 | |
| 17-18 | Включение В3 | 2802 | |
| 18-19 | Ожидание загорания Т2 и выключение В3 | 4002 |
В соответствии с формулой (10. 45) может быть определена функция плотности вероятности времени решения задачи f(τ), зная которую, с помощью выражений (10. 29) или (10. 32) можно найти вероятность своевременного решения задачи, если лимит времени на решение подобной задачи составляет tл:
ф
Не все характеристики выполнения отдельных операций τj и σj можно получить из справочных данных. В таком случае возникает необходимость получения недостающих данных. Наиболее точным мог бы быть экспериментальный метод, с помощью которого можно непосредственно измерить интересующие характеристики. Однако этот метод требует сложной и не всегда доступной регистрирующей аппаратуры. Поэтому он не всегда приемлем.
Возможен другой метод определения среднего значения и дисперсии времени выполнения отдельных операций, основанный на сочетании аналитического и экспериментального методов. Он предполагает проведение небольшого по объему эксперимента на аппаратуре любой сложности, имеющей однотипные с изучаемой аппаратурой органы управления и индикаторы, с последующим использованием математических зависимостей.
Сущность метода заключается в следующем [90, 98]. Предположим, имеется т задач, решаемых оператором. Каждая задача разбивается на m различных, но одних и тех же для каждой задачи типов элементарных операций. Обозначим через аij общее число операций j-го вида в i-й задаче. Тогда среднее значение времени решения i-й задачи равно:
ф (10.47)
Если решается m задач, то имеем систему т линейных алгебраических уравнений с т неизвестными τj (j = 1, 2, ..., m). Если при этом определитель системы отличен от нуля, система имеет единственное решение, в результате которого находят величины ¯τj.
Используя теорему о сложении дисперсий независимых величин, получим
| . ~Г • • • |
ф(10.48)
где Si2 — дисперсия времени решения i-й задачи:
σj2 — дисперсия времени выполнения j-й операции.
Решая систему т уравнений, можно определить дисперсии времени выполнения отдельных операций.
Практическое применение методики покажем на следующем примере. На экспериментальном пульте управления, представляющем собой набор сигнальных лампочек и кнопок, группе операторов предлагалось решить 4 задачи. Кроме кнопок, расположенных на пульте, имелась стартовая кнопка Ко, вынесенная на расстояние 40 смот пульта. Задачи эти следующие:
1. Исходное положение руки оператора на пульте управления. С приходом одного из двух сигналов оператор нажимает кнопку на пульте, затем Ко, а потом кнопку под горящей лампочкой.
2. Исходное положение руки на Ко. С поступлением одного из четырех сигналов оператор нажимает кнопку на пульте, затем Ко, а потом кнопку под горящей лампочкой.
3. Исходное положение руки на Ко. С приходом одного из восьми сигналов оператор нажимает кнопку под горящей лампочкой, а затем Ко.
4. Исходное положение на Ко. С приходом одного из двух сигналов оператор нажимает Ко и кнопку под горящей лампочкой.
Системы уравнений для определения средних значений и дисперсий времени выполнения элементарных операций имеют вид
ф (10.49)
где τ1 и σ12 — среднее значение и дисперсия латентного периода зрительной реакции;
τ2 и σ22 — среднее значение и дисперсия времени перемещения руки на расстояние 40 см;
τ3 и σ32 — среднее значение и дисперсия времени нажатия кнопки;
τ4 и σ42 — среднее значение и дисперсия времени переработки одной двоичной единицы информации;
Ti и Si2—среднее значение и дисперсия времени выполнения i-й задачи
(i =1, 2, 3, 4), находимые экспериментально.
Коэффициенты при τ4 и σ4 показывают количество перерабатываемой информации, которое для равновероятных сигналов равно:
ф(10.50)
где N — число альтернатив входного сигнала.
В результате эксперимента были определены средние значения и дне. Персии времени решения каждой из 4-х задач: Т1 = 1,52 сек; Т2 = 2,15 сек; Т3 = 1,98 сек; Т3 = 1,06 сек; S12 = 0,046 сек2; S22 = 0,071 сек2; S32 = 0,068 сек2; S42 = 0,032 сек2.
Аналитическое решение систем уравнений (10.49) дает следующие результаты:
τ1 = 0,19 сек; τ2 = 0,34 сек; τ3 = 0,12 сек; τ4 = 0,29 сек/бит; σ1 = 0,063 сек; σ2 = 0,105 сек; σ3 = 0,040 сек; σ4 = 0,098 сек/бит.
Эти значения довольно близки к результатам, опубликованным в литературе [17,40,44].
Системы уравнений, аналогичные (10.49), можно построить также для определения времени выполнения и других элементарных операций. Имея набор всевозможных значений τj и σj, можно оценить математическое ожидание и дисперсию времени решения оператором любой задачи управления, не прибегая каждый раз к эксперименту.
Дата добавления: 2015-12-10; просмотров: 1933;
