Понятие ансамбля моделей

Рассматривая нейросетевые модели, будем, прежде всего, иметь в виду классификаторы, но многие результаты справедливы и для регрессионных моделей. Построенная модель может допускать большое число ошибок. Говорят, что построена слабая модель [6]. Следует попытаться усовершенствовать модель, изменяя структуру нейронной сети, алгоритмы и параметры обу­чения. Но зачастую из‑за сложности задачи и низкого качества обучающих данных не удается достичь удовлетворительного качества работы модели. Тогда целесообразно применить набор моделей, применяемых совместно для решения единственной задачи. Такой набор моделей называется ансамблем (комитетом) моделей [6, 57–59]. В [33] используется термин "ассоциативные машины".

Можно выделить три причины, по которым ансамбль моделей может быть лучше отдельных моделей, входящих в ансамбль [59]:

1. Статистическая причина. Применение ансамбля моделей усредняет ошибку каждой отдельной модели и уменьшает влияние нестабильностей и случайностей при формировании гипотез. Решение задач классификации и регрессии представляет собой поиск гипотез о свойствах системы или о следующем состоянии системы. Для этого выдвигаются и оцениваются гипотезы. Выдвижение и оценка гипотез зависит от случайных факторов: разброс значений в наборе данных, выбор первой гипотезы, выбор последовательности обучающих примеров и т.д. Отдельно взятая модель часто находит и "доказывает" на обучающем множестве гипотезу, которая затем не показывает точности на примерах, не вошедших в обучающую выборку. Однако если использовать достаточно большое количество моделей, обученных примерно на одном и том же множестве примеров, то можно уменьшить нестабильность и случайность полученного результата путем комбинирования результатов (например, путем их усреднения, голосования и т.д.). Теоретически можно показать [57], что усреднение по множеству моделей, построенных на основе независимых обучающих множеств, всегда уменьшает ожидаемое значение среднеквадратической ошибки.

2. Вычислительная причина. Чаще всего нейронные сети обучаются градиентными алгоритмами, которые могут не попадать в точку глобального минимума функции ошибки, а попадать в точки локального минимума. Ансамбли моделей, обученных на различных подмножествах исходных данных, имеют бо́льший шанс найти глобальный оптимум, так как ищут его из разных начальных точек.

3. Репрезентативная причина. Комбинированная гипотеза может не находиться во множестве возможных гипотез для базовых классификаторов, т. е. строя комбинированную гипотезу, мы расширяем множество возможных гипотез.

Применяется несколько подходов к построению ансамблей моделей. Чаще всего ансамбль состоит из базовых моделей одного типа, которые обучаются на различных данных. Для формирования выхода ансамбля при опреде­ленных состояниях выходов моделей используют три подхода [6].

1. Голосование. Применяется в задачах классификации. Выбирается тот класс, который был выдан простым большинством моделей ансамбля.

2. Взвешенное голосование. Отличается от простого голосования назначением весов (баллов) для результатов разных моделей. Баллы учитывают точность работы разных классификаторов.

3. Усреднение (взвешенное или невзвешенное). Применяется при решении с помощью ансамбля за­дачи регрессии, когда выходы моделей будут числовыми. Выход всего ансамбля мо­жет определяться как простое среднее значение выходов всех моделей. Если производится взвешенное усреднение, то выходы моделей умножаются на соответствующие веса.

При применении одинаковых моделей чаще всего используют два алгоритма: Bagging и Boosting. В алгоритме Bagging исходные данные случайно разбиваются на одинаковые по размеру подмножества, каждое из которых используется для обучения одного базового классификатора. Прогноз ансамбля определяется большинством голосов или средним.

В алгоритме Boosting используется цепочка классификаторов, в которой каждый классификатор (кроме первого) основное внимание уделяет классификации примеров, неправильно классифицированных предшествующим классификатором. Результат ансамбля представляет собой взвешенное голосование прогнозов базовых классификаторов. Вес, с которым учитывается результат прогноза каждого базового классификатора при голосовании, соответствуют точности его прогнозирования.

Другим подходом к построению ансамбля является использование различных базовых алгоритмов, обучаемых на одинаковых данных [59]. После обучения базовых моделей, исходные данные вместе с результатами прогноза всех базовых моделей используются для обучения мета-алгоритма, который учится распознавать, на каких фрагментах данных следует доверять той или иной базовой модели. Такой подход к созданию ансамбля моделей называется Stacking.

Бэггинг

Термин "бэггинг" (bagging) происходит от английского словосочетания bootstrap aggregating, така для формирования выборок в этом методе применяется бутстреп (см. раздел 3.3 данной главы). Бэггинг основан на том, что многие классификаторы, параметры которых формируются в процессе обучения, в частности, нейронные сети, являются неустойчивыми [6]. Небольшие изменения в обучающем множестве могут привести к изменению модели (в случае нейронной сети — к изменению весов сети). Таким образом, обучая одинаковые нейронные сети на различных обучающих множествах, можно получить разные классификаторы. Объединяя результаты классификаторов с помощью голосования (или усреднения в случае регрессии) можно получить более точный результат, чем в случае одного классификатора.

Алгоритм бэггинга достаточно прост [6, 57–60]. Сначала из исходного множества данных с использование бутстрепа формируется столько обучающих выборок, сколько предполагается использовать классификаторов. Полученные выборки содержат такое же ко­личество примеров, что и исходное множество. Но, как было показано в разделе 3.3, набор примеров в этих выборках будет различным: одни примеры могут быть отобраны по нескольку раз, а другие — ни разу. Далее каждый классификатор обучается на своем обучающем множестве. Результат классификации получется путем голосования или простого усреднения (в случае регрессии).

Почему бэггинг уменьшает ошибки отдельных классификаторов? Эффект от применения бэггинга можно объяснить, представляя ошибку классификатора в виде суммы двух слагаемых: смещения и дисперсии [59–60]. Смещение — это ошибка конкретного обучающего алгоритма на бесконечном числе независимых обучающих примеров. Смещение не может равняться нулю, так как не существует идеальных классификаторов. Дисперсия — это ошибка, обусловленная конечными размерами обучающей выборки. Бэггинг, комбинируя нескольких классификаторов, позволяет уменьшить ошибку за счет уменьшения дисперсии.

Бэггинг обеспечивает повышение точности на всех задачах, наилучшие результаты достигаются при использовании неустойчивых моделей, к которым относятся нейронные сети.

Бустинг

Бустинг [61] (англ. boosting — улучшение) — это процедура последовательного построения классификаторов, когда каждый следующий классификатор стремится компенсировать недостатки предыдущих классификаторов. Ранний вариант бустинга строился по следующему алгоритму [5]:

Первый классификатор обучается на множестве из 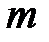примеров.

Второй классификатор обучается также на 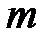примерах, выбираемых так, что первый классификатор ровно на половине из них дает точный ответ.

Третий классификатор обучается на таких 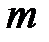примерах, которых мнения первого и второго классификатора расходятся.

Окончательный результат формируется голосованием по результатам трех классификаторов.

В настоящее время наиболее популярен алгоритм AdaBoost (Adaptive Boosting — адаптивное улучшение) [62]. Рассмотрим без доказательства алгоритм AdaBoost [58] (доказательство можно найти в [58–59]).

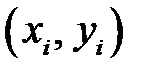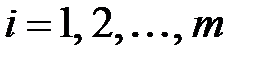Пусть дан набор примеров , где . Алгоритм состоит из ряда итераций. На каждой итерации строится классификатор, который обучается на исходном наборе примеров. Но в качестве функционала ошибки используется взвешенная ошибка

,

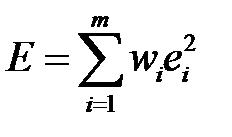где 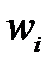— вес 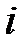‑го примера, вычисленный на предыдущей итерации, 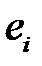— ошибка 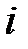‑го примера.

Причем веса правильно классифицированных примеров уменьшаются, а веса неправильно классифицированных примеров остаются без изменения. В результате на каждой итерации классификатор будет больше "внимания" уделять примерам, неправильно распознанным на предыдущих итерациях. Перед началом итераций веса примеров одинаковы: 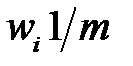. Итерации заканчиваются, когда функционал ошибки станет малым. Выход ансамбля формируется в результате взвешенного голосования. Причем веса классификаторов также зависят от ошибки. В результате алгоритм имеет вид.

В цикле, пока не выполнится критерий останова 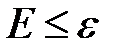, где 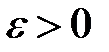— малое число, выполнить шаги 1–4:

1. Обучить классификатор, вычислить ошибку классификатора 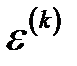( 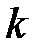— номер итерации) как сумму весов примеров, которые были классифицированы неправильно.

2. Вычислить вес классификатора

.

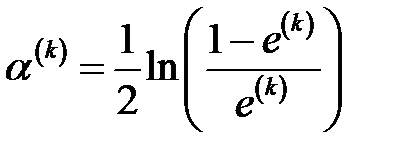3. Пересчитать веса правильно классифицированных примеров: 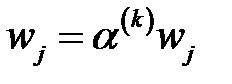, , 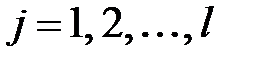где — число правильно классифицированных примеров.

4. Нормировать веса правильно классифицированных примеров

.

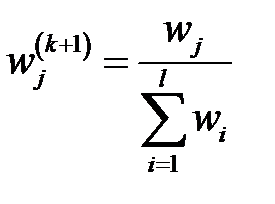При комбинировании выходов ансамбля веса всех классификаторов, которые одинаково классифицируют определенный класс (то есть имеют этот класс на выходе), суммируются и выбирается класс, набравший наибольшую сумму голосов.

На большинстве (но не на всех задачах) метод AdaBoost обеспечивает лучшие результаты, чем бэггинг. Метод прост в реализации. Интересно, что метод позволяет определять выбросы в обучающей выборке. Это примеры, веса которых в процессе обучения принимают наибольшие значения. Недостатком метода является в первую очередь то, что с увеличением числа итераций сеть обучается, в основном, на трудных для классификации примерах. Такие примеры обычно являются нетипичными или аномальными и обучение на них может привести к переобучению. Поэтому бустинг более склонен к переобучению, чем бэггинг. Бустинг требует для обучения более длинных обучающих выборок и может привести к построению громоздких композиций, содержащих большое число классификаторов.

Особо следует на опасности переобучения. Ансамбли моделей повышают точность обучения, но не гарантируют точность обобщения. Поэтому при построении ансамблей необходимо контролировать точность обобщения.

[1] Кохонен Т. Самоорганизующиеся карты. — М.: БИНОМ. Лаборатория знаний, 2008. — С. 11.

[2] В [32] компоненты вектора имеют противоположные знаки, это объясняется тем, что вычисляются коллинеарные собственные векторы.

[3] Вапник Владимир Наумович (1936) — крупный специалист в области машинного обучения. С 1990 г. работает в США. С 2003 г. является профессором колледжа Royal Holloway Лондонского университета и профессором Колумбийского университета в Нью-Йорке.

Червоне́нкис Алексей Яковлевич (1938–2014) — российский ученый, ведущий сотрудник Института проблем управления им. В. А. Трапезникова РАН, профессор колледжа Royal Holloway Лондонского университета.