ОТНОСИТЕЛЬНЫЙ ПОКОЙ ЖИДКОСТИ

Сведения из теории

Под относительным покоем понимается такое состояние, при котором в движущейся жидкости отдельные частицы не смещаются одна относительно другой. При этом жидкость перемещается как твердое тело. Само движение жидкости в этом случае можно назвать переносным движением. Для этого состояния характерно постоянство формы объема жидкости. Очевидно, что рассматриваемая масса жидкости будет неподвижна в координатной системе, связанной с движущимся резервуаром.

На жидкость, находящуюся в относительном покое, действуют массовые силы (силы тяжести и силы инерции переносного движения), а из поверхностных – силы давления.

Рассмотрим два частных случая относительного покоя: покой при переносном прямолинейном движении и покой при переносном вращательном движении вокруг вертикальной оси.

3.1.1. Относительный покой при прямолинейном движении на наклонной плоскости

Рассмотрим движение резервуара с жидкостью с постоянным ускорением a по наклонной плоскости, образующей угол a с горизонтальной плоскостью (рис. 3.1).

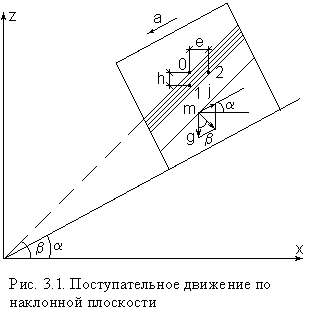Жидкость в движущемся резервуаре находится под действием силы давления, силы тяжести и силы инерции переносного движения. Ускорение силы инерции 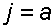и направлено в сторону, обратную ускорению резервуара a. Результирующий вектор массивных сил определяется диагональю параллелограмма, построенного на ускорениях сил тяжести g и инерции j.

Элемент поверхности равного давления перпендикулярен к диагонали параллелограмма и образует с горизонтом угол b , тангенс, которого равен

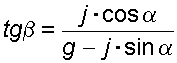(3.1)

Таким образом, поверхности равного давления, образуют семейство параллельных плоскостей с углом наклона к горизонту b .

Необходимо учесть, что если резервуар движется равномерн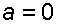о , то 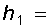и следовательно 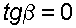и 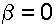. В этом случае поверхности равного давления представляют семейство горизонтальных плоскостей.

Если резервуар перемещается под действием силы тяжести (сила трения резервуара о плоскость равна 0), то 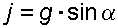, , 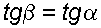, 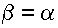а поверхности равного давления образуют семейство плоскостей, параллельных плоскости скатывания.

Если резервуар перемещается с ускорением, но вертикальн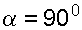о ( ), то 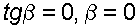, а поверхности равного давления образуют семейство горизонтальных плоскостей.

Найдем закон распределения давления в вертикальной плоскости 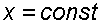. Учитывая, что система координат перемещается вместе с резервуаром, 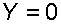, а для выбранной плоскости и 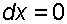, уравнение (2.6) примет вид:

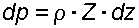. (3.2)

В этом случае .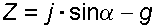

Тогда

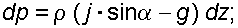
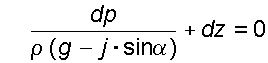(3.3)

После интегрирования имеем:

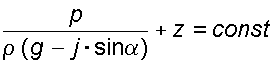(3.4)

Для двух точек 0 и 1 с координатам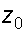и и 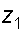имеем:

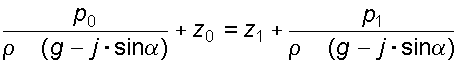(3.5)

или

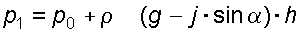. (3.6)

По аналогии получаем распределение давления в горизонтальной плоскости:

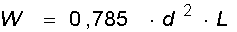, (3.7)

если 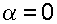, то имеем

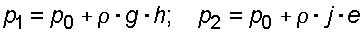, (3.8)

а свободная поверхность имеет угол наклона к горизонту (3.1)

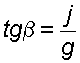. (3.9)

При свободном падении резервуара 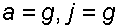и 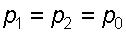, то есть во всем объеме давление одинаково.