Относительный покой при вращении вокруг вертикальной оси

В этом случае на жидкость действуют силы давления, силы тяжести и силы инерции переносного вращательного движения ускорения массовых сил будут равны:

Дифференциальное уравнение (2.8) примет вид:

(3.10)

После интегрирования, с учетом, что 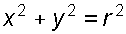получим:

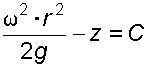(3.11)

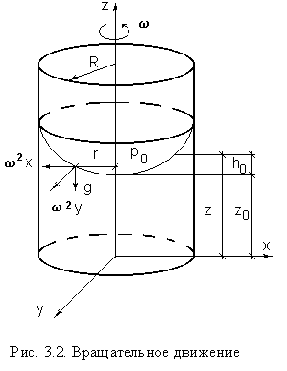
Уравнение (3.11) является уравнением параболоида вращения, а поверхности равного давления образуют семейство параболоидов вращения, сдвинутых вдоль вертикальной оси. Каждый параболоид характеризуется некоторым значением постоянной С. Для параболоида свободной поверхности принимаем, что при 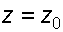(рис. 3.2) ,
поэтому . Тогда уравнение свободной поверхности примет вид:

(3.12)

или (3.13)

Закон распределения давления по объему жидкости получим из уравнения (2.6), подставив в него соответствующие значения X, Y и Z. После интегрирования получаем:

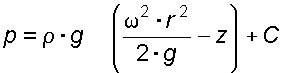. (3.14)

Постоянную интегрирования 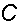определим из условия, что пр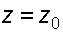и и 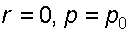, т.е. 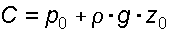. После подстановки в (3.14) окончательно имеем:

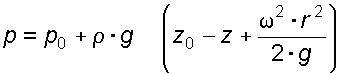. (3.15)

Для частиц жидкости расположенных на одной вертикали можем записать:

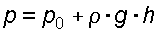(3.16)

где

,

т.е. существует обычный гидростатический закон распределения давления.