Примеры решения задач. Пример 1. Сосуд с прямоугольным основанием наполнен водой до высоты h и движется по горизонтальной поверхности с ускорением a (рис
Пример 1. Сосуд с прямоугольным основанием 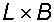 наполнен водой до высоты h и движется по горизонтальной поверхности с ускорением a (рис. 3.3). Определить избыточное давление воды на дно сосуда у передней и задней стенок в точках 1 и 2.
наполнен водой до высоты h и движется по горизонтальной поверхности с ускорением a (рис. 3.3). Определить избыточное давление воды на дно сосуда у передней и задней стенок в точках 1 и 2.
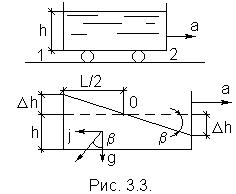 Решение: При горизонтальном движении сосуда с ускорением a свободная поверхность жидкости станет наклонной к горизонту под углом b . Так как
Решение: При горизонтальном движении сосуда с ускорением a свободная поверхность жидкости станет наклонной к горизонту под углом b . Так как 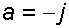 , то
, то 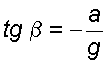 . Учитывая что объем воды не изменяется, поэтому свободная поверхность повернется вокруг оси О, расположенной на середине длины сосуда, а повышение и понижение свободной поверхности у торцовых стенок будет одинаковым и равным
. Учитывая что объем воды не изменяется, поэтому свободная поверхность повернется вокруг оси О, расположенной на середине длины сосуда, а повышение и понижение свободной поверхности у торцовых стенок будет одинаковым и равным 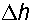 .
.
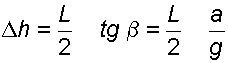 .
.
Избыточное давление в точке 1 будет равно:
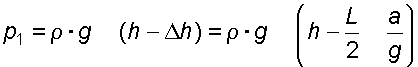 .
.
В точке 2 избыточное давление составит:
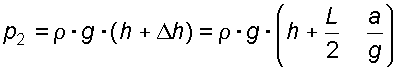 .
.
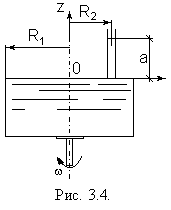
Пример 2. Цилиндрический сосуд радиусом R1 наполнен жидкостью плотностью r до уровня a в открытой трубке малого диаметра, установленной на крышке сосуда на расстоянии R2 от центра, и приведен в равномерное вращение относительно центральной вертикальной оси (рис. 3.4). Определить угловую скорость вращения сосуда, при которой избыточное давление под крышкой в центре сосуда будет равно 0.
 Решение: Используя уравнение (3.15) найдем закон распределения избыточного давления в жидкости, заполняющей сосуд, учитывая что
Решение: Используя уравнение (3.15) найдем закон распределения избыточного давления в жидкости, заполняющей сосуд, учитывая что 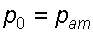
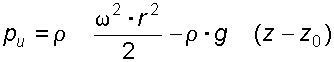
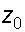 находим, используя граничное условие:
находим, используя граничное условие: 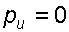 при
при 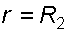 и
и 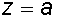
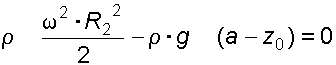
откуда
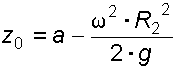 .
.
Подставляя, 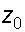 получим искомый закон распределения давления.
получим искомый закон распределения давления.
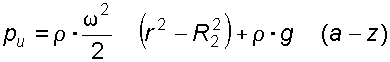 .
.
Для точек на поверхности крышки 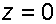 имеем
имеем
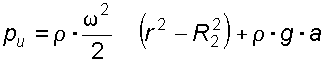 .
.
Искомую угловую скорость вращения определяем из условия 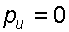 при
при 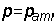
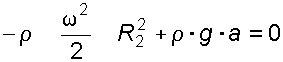 ,
,
откуда
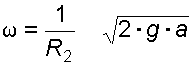 .
.
Дата добавления: 2015-12-08; просмотров: 4157;
