Распределение Пуассона. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Если число испытаний n велико, а вероятность события р мала (р≤0,1), для вычисления вероятности появления события А ровно k раз пользуются асимптотической формулой Пуассона.
Поставим задачу следующим образом: найти закон распределения случайной величины X – числа появления события А в n испытаниях. Для ее решения требуется определить возможные значения X и их вероятности. Очевидно, событие А в п испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, ..., либо n раз. То есть, случайная величина X может принимать следующие значения: х1=0, х2=1, х3=2,…, хn+1 = п. Для определения вероятности того, что в n опытах случайная величина Х примет значение х=m, можно воспользоваться формулой Бернулли:
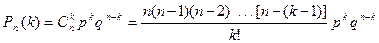
После преобразований при np=λ=const (см. раздел 1.12.5) получим
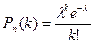 (3.3)
(3.3)
Пример 3.2. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0, 0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.
Решение. Поставленную задачу можно сформулировать в следующем виде: найти вероятность того, что случайная величина Х – число поврежденных в пути изделий равно 3. Воспользуемся асимптотической формулой Пуассона. По условию n=5000, p=0,0002, k =3. Найдем λ=np=5000∙0,0002=1.
По формуле Пуассона искомая вероятность приближенно равна
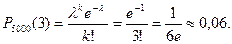
Дата добавления: 2015-11-06; просмотров: 1026;
