ДР-2.3 (Письменный, с. 77, № 2.4)
Дисперсия.
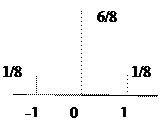
Итак, математическое ожидание является тем «средним» значением, вокруг которого распределены все возможные значения случайной величины. Однако знание среднего значения случайной величины для большинства задач недостаточно, так как значения случайных величин при одинаковом среднем могут быть совершенно разными, например, одна может меняться в узких пределах, а вторая – в широких. То есть, случайные величины могут иметь разные разбросы относительно их математического ожидания. Приведем в качестве примера графики некоторых распределений, имеющих одинаковое среднее, равное нулю, и разные разбросы (рис.2.3).
На всех графиках нас интересует разброс СВ вокруг среднего (в нашем примере оно равно нулю; если это не так, картинка только сдвигается).
Следовательно, необходимо иметь еще количественную характеристику разброса возможных значений случайной величины относительно математического ожидания. Для этого рассмотрим разность(х– а) – отклонение возможного значения случайной величины от ее математического ожидания. Однако, знание просто величины разброса СВ недостаточно, нужно ещё оценить, с какой вероятностью этот разброс достигается.
Чтобы охарактеризовать разброс, рассеяние случайной величины, используются несколько показателей, но чаще всего применяют дисперсию D(Х) или среднеквадратическое (стандартное) отклонение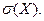 
 | ||||||||||||||
 | ||||||||||||||
 | ||||||||||||||
 |
|
| ||||||||||||
 | ||||||||||||||
 | ||||||||||||||
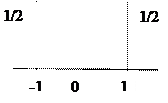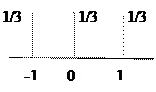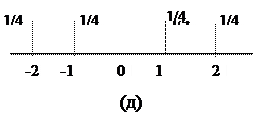Рис. 2.3
Дисперсией случайной величины Х называется математическое ожидание квадрата отклонения СВ от ее математического ожидания
D(ξ) = M((ξ – a)2) (2.9)
или для ДСВ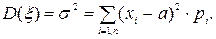 
(2.10)
Для вычисления дисперсии часто оказывается полезной формула
D(ξ) = M(ξ)2 – (М(ξ ))2, (2.11)
для ДСВ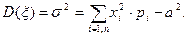 
(2.12)
Действительно
D(ξ) = M((ξ – a)2) = M(ξ2 – 2aξ + a2) = M(ξ2) - M(2aξ) + M(a2) =
= M(ξ2) - 2a M(ξ) + a2 = M(ξ2) - 2a2 + a2 = M(ξ2) - a2 = M(ξ2) – (M(ξ2)) 2.
Пример 2.11.Вычислим дисперсии распределений, приведенных на рис. 2.3:
а) 1∙ 1/8 + 1∙ 1/8 – 0 = 1/4 = 0,25;
б) 1∙ 1/3 + 1∙ 1/3 – 0 = 2/3 = 0,(6);
в) 1∙ 1/2 + 1∙ 1/2 – 0 = 1;
г) 4∙ 1/2 + 4∙ 1/2 – 0 = 4;
д) 4∙ 1/4 + 1∙ 1/4 + 1∙ 1/4 + 4∙ 1/4 – 0 = 2,5.
Самая большая дисперсия у 4-го распределения, когда все значения удалены от среднего на расстояние 2. Самая маленькая – у первого, когда математическое ожидание является наиболее вероятным значением.
Свойства дисперсии
1. Дисперсия постоянной величины равна нулю D(C) = 0 (2.13)
Действительно: D(C) = М(С2) – (М(С))2 = С2 – С2 = 0.
2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат D(C∙Х) = С2 ∙ D(Х) (2.14)
Действительно: D(C∙Х) = М(С2∙Х2) – (М(С∙Х))2 = С2 М(Х2) – С2 ∙(М(Х))2 =
= С2 (М(Х2) –(М(Х))2) = С2 D(Х).
3. Дисперсия суммы (разности) конечного числа независимых в совокупности случайных величин равна сумме дисперсий слагаемых
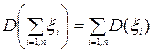(2.15)
Поскольку размерность дисперсии случайной величины равна квадрату размерности самой случайной величины, то в ряде случаев удобнее пользоваться корнем из дисперсии. Эта характеристика имеет ту же размерность, что и сама случайная величина, и ее называют среднеквадратическим отклонением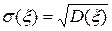 
(2.16)
Для распределений, приведённых на рис. 2.3, значения среднеквадратического отклонения равны: а) σ = 0,500; б) σ = 0,816; в) σ = 1,000; г) σ = 2,000; д) σ = 1,581. Отметим, что для четвертого распределения (рис. 2.3 - г), где все значения находились на расстоянии 2 от среднего, среднеквадратическое отклонение принимает наибольшее значение σ = 2.
Из свойств дисперсии немедленно следуют свойства среднеквадратического отклонения: σ(С) = 0; σ(С∙ξ) =|C|∙σ(ξ).
Домашнее задание: ДР-2.4 и 2.5 (Письменный, с. 83-84, № 1 и 2)
Дата добавления: 2015-11-06; просмотров: 1019;