Непрерывные случайные величины

Непрерывная случайная величинаХ в отличие от дискретной может принимать любое значение из некоторого промежутка, т.е. её значения сплошь заполняют некоторый интервал и потому их множество несчётно.

Например:

1) размер детали массового производства;

2) урожай с одной сотки;

3) ошибка измерения;

4) путь, пройденный автомобилем к данному моменту времени.

Важнейшей характеристикой непрерывной случайной величины Х помимо функции распределения F(x)=p(ξ<x), является плотность распределения вероятности.

Плотностью распределения вероятности или плотностью вероятности непрерывной случайной величины Х называется производная ее функции распределения, то есть 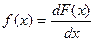. (2.17)

В точках, где производная функции F(x) не определена, будем считать, что f(x)=0.

Полезно помнить, что плотность вероятности f(x) это есть ΔР/Δх – вероятность попадания Х в интервал (х, х+ Δх), деленная на его длину Δх, когда длина Δх исчезающее мала, то есть

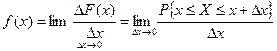(2.18)

Плотность распределения обладает следующими свойствами:

1. В силу того, что функция F(x) монотонно возрастает, её плотность f(x) всюду неотрицательная, т.е. f(x) ≥ 0.

2. Функция распределения НСВ может быть выражена через ее плотность вероятности по формуле

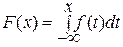(2.19)

То есть, зная F(x), можем найти плотность вероятности по формуле

f(x) = F'(x), а зная f(x), найдем функцию распределения по формуле (2.19).

3. Вероятность попадания НСВ в промежуток [a, b] равна определенному интегралу от ее плотности в пределах от a до b, т.е.

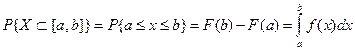(2.20)

4. Интеграл от плотности вероятности НСВ в бесконечных пределах равен единице, т.е.

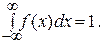(2.21)

то есть, вся площадь между графиком f(x) и осью Ох равна 1:

(аналог формулы нормирования (2.1) для непрерывной СВ).

Для непрерывныхслучайных величинматематическое ожидание определяется как: 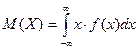(2.22)

а дисперсия 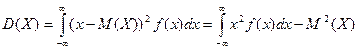(2.23)

Все рассуждения, приведенные для математического ожидания и дисперсии дискретных случайных величин, верны и для непрерывных величин.

В качестве примера непрерывного распределения мы рассмотрим так называемое нормальное распределение.

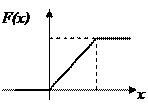Пример 2.12. Найти математическое ожидание и дисперсию непрерывной случайной величины Х, заданной функцией распределения

0 при х ≤ 0,

F(x) = x при 0 < x ≤ 1,

1 при x > 1.

0 при х ≤ 0,

f(x) = F′(x) = 1 при 0 < x ≤ 1,

0 при x > 1.

Найдём математическое ожидание по формуле (2.22)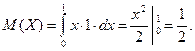

Найдём дисперсию по формуле (2.23)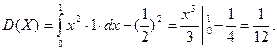

Домашнее задание: ДР-2.6 (Гмурман, с. 126, № 2)