Гипергеометрическое распределение
Прежде чем дать определение гипергеометрическогораспределения, рассмотрим задачу. Пусть в партии из N изделий имеется М стандартных (М < N). Из партии случайно отбирают п изделий (каждое изделие может быть извлечено с одинаковой вероятностью), причем отобранное изделие перед отбором следующего не возвращается в партию (поэтому формула Бернулли здесь неприменима). Обозначим через X случайную величину -число m стандартных изделий среди п отобранных. Очевидно, возможные значения X таковы: 0, 1, 2, …, min (М, п).
Найдем вероятность того, что Х = т, т. е. что среди n отобранных изделий ровно т стандартных. Используем для этого классическое определение вероятности. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь п изделий из N изделий, т. е. числу сочетаний 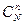 .
.
Найдем число исходов, благоприятствующих событию Х= т, (то есть, что среди взятых п изделий ровно т стандартных); m стандартных изделий можно извлечь из М стандартных изделий 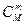 способами; при этом остальные n-т изделий должны быть нестандартными; взять же п—т нестандартных изделий из N-т нестандартных изделий можно
способами; при этом остальные n-т изделий должны быть нестандартными; взять же п—т нестандартных изделий из N-т нестандартных изделий можно 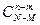 способами. Следовательно, число благоприятствующих исходов равно
способами. Следовательно, число благоприятствующих исходов равно 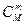
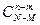 (правило умножения).
(правило умножения).
Искомая вероятность равна отношению числа исходов, благоприятствующих событию X = m, к числу всех элементарных исходов
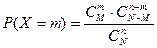 (3.6)
(3.6)
Формула (3.6) определяет распределение вероятностей, которое называют гипергеометрическим.
Учитывая, что m - случайная величина, заключаем, что гипергеометрическое распределение определяется тремя параметрами: N, М, п. Иногда в качестве параметров этого распределения рассматривают N, п и p=M/N, где р—вероятность того, что первое извлеченное изделие стандартное.
Заметим, что если п значительно меньше N (практически если п<0,1N), то гипергеометрическое распределение дает вероятности, близкие к вероятностям, найденным по биномиальному закону.
Пример 3.4.Среди 50 изделий 20 окрашенных. Найти вероятность того, что среди наугад извлеченных 5 изделий окажется ровно 3 окрашенных.
Решение. По условию, N = 50, M = 20, n = 5, m = 3. Искомая вероятность
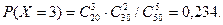
Дата добавления: 2015-11-06; просмотров: 763;
