Свойства математического ожидания

1. Математическое ожидание постоянной равно самой постоянной

М(С) = С. (2.5)

Действительно постоянную С можно рассматривать как дискретную случайную величину, принимающую единственное значение С с вероятностью 1, поэтому М(С)=1∙С=С.

2. Постоянный множитель можно выносить за знак математического ожидания М(С∙ξ) = С∙М(ξ) (2.6)

Поскольку при умножении на С возможные значения случайной величины также умножаются на С, при сохранении соответствующих вероятностей, то (2.6) следует из известных свойств суммы и интеграла.

Следующие свойства приведем без обоснования.

3. Математическое ожидание суммы конечного числа случайных величин равно сумме математических ожиданий слагаемых

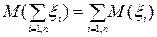(2.7)

4. Математическое ожидание произведения конечного числа независимых в совокупности случайных величин равно произведению математических ожиданий сомножителей

М(ξ₁∙ξ₂∙ … ∙ξ_n) = М(ξ₁)∙М(ξ₂)∙ … ∙М(ξ_n) (2.8)

Пример 2.9. Задачу о страховке (пример 2.8) решим другим способом.

Считаем, что есть две случайные величины: Y – выигрыш 200 рублей с вероятностью 1 и Z – возможность проиграть 10000 рублей с вероятностью 0,01. Доход компании - случайная величина X = Y + Z.

Для взноса 200 рублей:

MX = MY + MZ = - 10000∙0,01 + 200 = 100;

Для взноса 100 рублей:

MX = MY + MZ = - 10000∙0,01 + 100 = 0. (справедливая игра).

Пример 2.10. Фермер считает, что принимая во внимание различные потери и колебания цен, он сможет выручить не более 60 центов за десяток яиц, потерять не более 20 центов за десяток и что вероятности возможных выигрышей и потерь таковы:

Как оценить ожидаемую прибыль от продажи десятка яиц; от ожидаемых им в этом году 10 000 яиц?

Решение. Х – случайная величина, прибыль от продажи 10 яиц.

МХ = 0,6∙0,2 + 0,4∙0,5 +0,2∙0,2 + 0∙0,06 - 0,2∙0,04 = 0,352.

М10000Х = 10000∙0,352 = 3520$.

Домашнее задание: ДР-2.2 (Гмурман, с. 83, № 3)