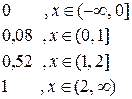Функция распределения ДСВ и ее свойства
Случайные величины
Наряду со случайными событиями одним из основных понятий теории вероятностей является понятие случайной величины.
Случайнойназывают величину, которая в результате испытания может принять одно и только одно численное значение, заранее не известное и зависящее от случайных факторов, которые заранее не могут быть учтены.
Примерами случайных величин могут быть: 1) число очков, выпадающих при бросании игрального кубика - целое, положительное число от 1 до 6; 2) число выстрелов до первого попадания в цель – также целое положительное число от 1 до ∞; 3) расстояние, которое пролетит снаряд при выстреле из орудия положительное вещественное число из некоторого промежутка (а, b).
Обозначают случайные величины прописными буквами латинского алфавита X, Y, Z и другими [в некоторых учебниках - греческими буквами – ξ (кси), η (эта), ζ (дзета) и другими], а их возможные значения – х, у, z, снабжая их при необходимости индексами.
В зависимости от возможных значений все случайные величины можно разбить на два типа: дискретные и непрерывные.
Дискретной называют случайную величину, которая принимает отдельные, изолированные одно от другого возможные значения, между которыми нет других возможных значений этой случайной величины. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Например: 1) число, выпавшее при игре в рулетку – целые положительные числа, равные 0, 1, 2, …, 38; 2) число выстрелов до первого попадания в цель – также целое положительное число от 1 и более.
Непрерывной называют случайную величину, которая может принимать все возможные значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно. Например, путь, пройденный автомобилем за данный промежуток времени.
Дискретные случайные величины.
Функция распределения ДСВ и ее свойства
Две случайные величины могут иметь одинаковые возможные значения, но принимать их с различными вероятностями (например, оценки на экзамене у сильных и слабых студентов могут иметь одинаковые возможные значения, но с разными вероятностями). То есть, для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, необходимо еще указать и вероятности, с которыми она может их принимать.
Для установления связи между значениями случайной величины и их вероятностями вводят понятие закона распределения.
Законом распределения дискретной случайной величины называют правило, по которому каждому возможному значению xi ставится в соответствие вероятность pi, с которой случайная величина Х может принять это значение.
Закон распределения дискретной случайной величины может быть задан графически, аналитически и таблично. В последнем случае задается таблица, где в одной строке записаны все возможные значения xi, а в другой - соответствующие им вероятности pi: X x1 x2 . . . xn
P p1 p2 . . . pn
Поскольку в результате опыта случайная величина может принять одно и только одно из возможных значений, то события, заключающиеся в том, что Х примет значение х1, х2, …, хn попарно несовместны и в сумме образуют достоверное событие, то есть 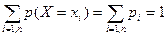 (2.1)
(2.1)
Задача 2.1. Абитуриент сдает два вступительных экзамена: по математике и физике. Составить закон распределения случайной величины Х - числа полученных пятерок, если вероятность получения пятерки по математике равна 0,8, по физике – 0,6.
Решение. Пусть А1 и А2 - события, заключающиеся в том, что и математика, и физика, соответственно, сданы на «5». Очевидно, возможные значения ξ – количества «пятерок» есть 0, 1, 2, причем
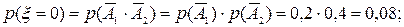

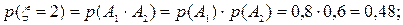
При вычислении вероятностей использовались несовместность слагаемых и независимость (рис. 2.1) сомножителей. Сведем полученные данные в таблицу
| Х | |||
| Р | 0,08 | 0,44 | 0,48 |
Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (хi, рi), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
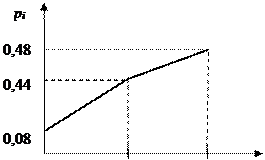
Для рассматриваемого примера
многоугольник распределения имеет вид:
| |
| |
|
| |
Рис. 2.1.
Задача 2.2. Вероятность появления события А при одном испытании равна р. Испытания повторяются до появления события А. Составить закон распределения случайной величины ξ – числа испытаний, проведенных до первого появления А.
Решение. Возможные значения Х–целые числа от 1 до ∞. Предположим, что Х = n и найдем вероятность такого события. Очевидно, оно произойдет, если в первых n-1 испытаниях произойдут события 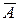 , а в (n+1)-ом испытании произойдет событие А. Отсюда, искомая вероятность равна
, а в (n+1)-ом испытании произойдет событие А. Отсюда, искомая вероятность равна 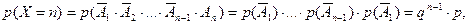
Здесь q =1- p и мы воспользовались независимостью сомножителей.
Задача 2.3.Вденежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины X - стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение. Напишем возможные значения X: х1 = 50, х2= 1, х3 = 0. Вероятности этих возможных значений таковы: р1 = 0,01; р2 = 0,1; p3=l-(р1 + р2) = 0,89. I
Напишем искомый закон распределения: X 50 1 0
р 0,01 0,1 0,89
Контроль: 0,01+0,1+0,89=1.
Задача 2.4. (Письм., с.63). В урне 8 шаров, из которых 5 белых, остальные – черные. Из нее вынимают наугад 3 шара. Найти закон распределения числа белых шаров в выборке.
Решение. Возможные значения С.В. Х – числа белых шаров в выборке есть х1=0, х2=1, х3=2, х3=3. Вероятности их, соответственно, будут
|
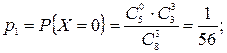
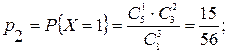
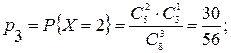
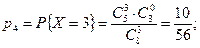
| Х | ||||
| Р | 1/56 | 15/56 | 30/56 | 10/56 |
(Контроль: 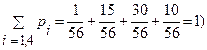
Для задания любой случайной величины можно ввести понятие функции распределения.
Функцией распределения случайной величины Х называется функция F(x), которая для любого числа х равна вероятности того, что случайная величина Х примет значение, меньшее х: F(x) = p(Х < x). …. .(2.2)
При известном законе распределения функция распределения дискретной случайной величины имеет вид: 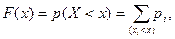 (2.3)
(2.3)
где (xi<x) означает, что суммирование ведется по всем индексам i, для которых это неравенство выполняется.
Функция распределения ДСВ обладает следующими свойствами:
1. Функция распределения F(x) ограничена, т.е. 0≤ F(x) ≤ 1.
2. Функция распределения – неубывающая функция на множестве R,
т.е., если х2 > х1, то F(x2) ≥ F(x1).
3. Функция распределения обращается в ноль на минус бесконечности и равна единице в плюс бесконечности, т.е. F(- ∞) = 0, F(+ ∞) = 1.
4. Вероятность попадания случайной величины Х в промежуток [a, b) равна приращению функции распределения на этом промежутке, т.е.
Р{a ≤ X ≤ b} = F(b) - F(a)
5. Функция распределения непрерывна слева, т.е.
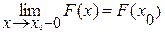
Функция распределения F(x) дискретной случайной величины Х является ступенчатой, сохраняющей постоянное значение на каждом интервале, не содержащем точек xi, и терпящей в этих точках скачок, равный pi.
Для задачи 2.1 о количестве пятерок функция распределения ДСВ и ее график (рис. 2.2) представлены ниже
 | |||||
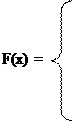 | |||||
| |||||
Рис. 2.2.
Домашнее задание: ДР-2.1
Дата добавления: 2015-11-06; просмотров: 8117;