Линейные дифференциальные уравнения.

Дифференциальное уравнение первого порядка называется линейным, если оно представлено в виде

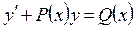(13.10)

Отметим, что искомая функция y и ее производная y' входят в уравнение в первой степени. Функции непрерывны в рассматриваемой области. Если Q(x)=0, уравнение называется однородным, в противном случае - неоднородным.

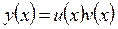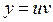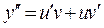Будем искать решение уравнения (13.10) в виде произведения двух функций, то есть , из которых одна (любая) может быть выбрана произвольно. Если , то . Из (13.10) получаем

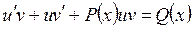или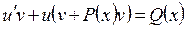

Пусть функция V(x) удовлетворяет условно

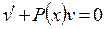, (13.11)

тогда 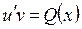(13.12)

Получены уравнения с разделяющимися переменными, которые позволяют найти u(x) и v(x)

Пример. Решить уравнение .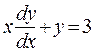

Запишем уравнение в стандартной форме .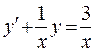

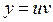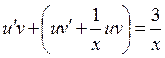Если , то или .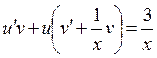

Полагая 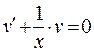, получаем .

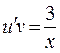Решим уравнение ,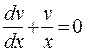

ограничившись его частным решением, так как v(x) может быть выбрана, как сказано выше, произвольно. Разделяя переменные и интегрируя это уравнение, получаем 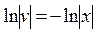. Тогда 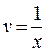. Из условия 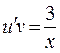, с учетом найденной функции 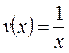приходим к уравнению

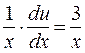или ,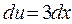

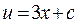
Таким образом, общее решение данного дифференциального уравнения имеет вид:

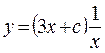или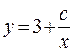

Геометрически оно представляет собой семейство гипербол.

1 2 34

Дата добавления: 2015-11-06; просмотров: 1457;