Дифференциальные механизмы
Дифференциальные механизмы имеют зубчатые колёса с подвижными осями (рис.6.5).
 Зубчатое колесо 1 называется центральным колесом, колесо 2, имеющее подвижную ось, – сателлитом, а звено H, несущее сателлит, – водилом. Число степеней подвижности механизма находим по формуле Чебышева
Зубчатое колесо 1 называется центральным колесом, колесо 2, имеющее подвижную ось, – сателлитом, а звено H, несущее сателлит, – водилом. Число степеней подвижности механизма находим по формуле Чебышева
W= 3n-2p1-p2= 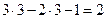 ,
,
здесь n=3 – число подвижных звеньев (колёса 1 и 2 водило H),
p1=3 – число одноподвижных кинематических пар (стойка – колесо 1, стойка - водило H и водило H – колесо 2,
p2=1 - число двухподвижных кинематических пар (зубья колёс 1 и 2).
В данном механизме два независимых закона движения, т.е. двум звеньям можно задать произвольные законы движения, тогда звено 2 будет двигаться по определённому закону.
Рис.6.5
Метод обращённого движения
Дифференциальные механизмы не имеют постоянного передаточного отношения. Передаточное отношение можно определить, используя метод обращённого движения (метод Виллиса). Для этого дифференциальному механизму придаём дополнительную угловую скорость, равную угловой скорости водила 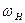 , но направленную противоположно. Это не изменяет относительного движения звеньев, абсолютные же скорости будут другими.
, но направленную противоположно. Это не изменяет относительного движения звеньев, абсолютные же скорости будут другими.
| Звено | Н | ||
| Скорость звена | 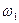
| 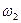
| 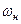
|
| Скорость при обращённом движении | 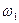 - - 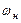
| 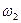 - - 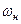
|
Такой дифференциальный механизм называется преобразованным, для которого справедливо отношение:

 (6.2)
(6.2)
Если в дифференциальном механизме имеется n зубчатых колёс:
 =
= 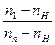 (6.3)
(6.3)
Дата добавления: 2015-10-13; просмотров: 750;
