Эффективность рекламы.
Задачи, приводящие к понятию дифференциального уравнения.
Математическая модель демографического процесса;
Известно, что население любой страны подвержено изменениям во времени. Этому способствуют различные процессы, протекающие в стране и мире (экономические, политические и др.)
Для оптимального планирования экономики необходимо учитывать демографические процессы, происходящие в обществе (в данном регионе или в стране в целом). В таком случае требуется найти закон изменения численности населения с течением времени.
Пусть население в произвольный момент времени t равно y(t). Будем полагать, что промежутку времени 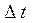 соответствует прирост населения
соответствует прирост населения 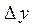 .Очевидно, этот прирост пропорционален количеству населения y(t) в момент времени t и промежутку времени
.Очевидно, этот прирост пропорционален количеству населения y(t) в момент времени t и промежутку времени 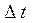 ,то есть
,то есть 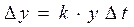 откуда
откуда  . Переходя к пределу при
. Переходя к пределу при  , получаем уравнение
, получаем уравнение
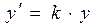 , (13.1)
, (13.1)
которое описывает в самом общем виде демографический процесс.
Отметим, что это уравнение содержит искомую функцию y(t) и ее производную y'.
Эффективность рекламы.
Предположим, торговой фирмой реализуется некоторая продукция B, о которой из числа Nпотенциальных покупателей знает yпокупателей. Для ускорения сбыта продукции были даны рекламные объявления по радио и телевидению. Информация о продукции распространяется среди покупателей посредством общения друг с другом. Для достижения оптимального сбыта товара требуется найти закон изменения числа граждан, владеющих информацией о продукции с течением времени. Естественно предположить, что после рекламных объявлений скорость изменения числа граждан, владеющих информацией о товаре B в момент времени t, пропорциональна как числу y(t) таких граждан, так и числу 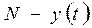 , которые о нем ничего не знают, то есть получаем уравнение
, которые о нем ничего не знают, то есть получаем уравнение
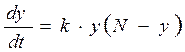 , (13.2)
, (13.2)
которое описывает процесс распространения рекламы среди населения. Уравнение (13.2) также как и уравнение (13.1), содержит,  наряду с искомой функцией y(t) и ее производную
наряду с искомой функцией y(t) и ее производную 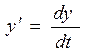 .
.
Дифференциальные уравнения. Основные понятия.
 Определение 1. Уравнение, связывающее независимые переменные xi, искомую функцию yи производные различных порядков этой функции, называется дифференциальным уравнением.
Определение 1. Уравнение, связывающее независимые переменные xi, искомую функцию yи производные различных порядков этой функции, называется дифференциальным уравнением.
Если искомая функция y зависит только от одной переменной, то дифференциальное уравнение называется обыкновенным и записывается в виде
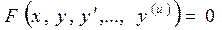 , (13.3)
, (13.3)
Порядок старшей производной, входящий в уравнение, называется порядком дифференциального уравнения. В частности, уравнение 1-го порядка имеет вид 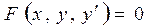 (13.4)
(13.4)
Рассмотрим дифференциальные уравнения 1-го порядка.
Простейшим дифференциальным уравнением1-го порядка является отыскание первообразной функции f(x). Действительно, если 
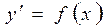 , то
, то
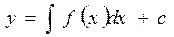 (13.5)
(13.5)
В данном случае дифференциальное уравнение имеет бесчисленное множество (семейство) решений. Задача отыскания решения всякого дифференциального уравнения сводится к отысканию всех его решений. Эта задача называется интегрированием дифференциального уравнения.
Из решения (13.5) обнаруживаем, что оно содержит произвольную постоянную C.
 Определение. Функция
Определение. Функция  называется решением дифференциального уравнения, если при подстановке ее в уравнение вместе о своей производной обращает его в тождество, то есть
называется решением дифференциального уравнения, если при подстановке ее в уравнение вместе о своей производной обращает его в тождество, то есть

При каждом фиксированном значении постоянной  , получаем некоторое решение
, получаем некоторое решение  , называемое частным решением.
, называемое частным решением.
 Определение. Совокупность функций
Определение. Совокупность функций 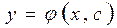 , где с - произвольная постоянная, всех частных решений называется общим решением дифференциального уравнения 1-го порядка.
, где с - произвольная постоянная, всех частных решений называется общим решением дифференциального уравнения 1-го порядка.

 Всякое частное решение
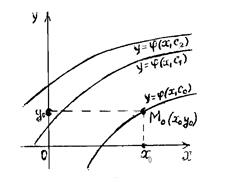
Всякое частное решение 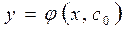 геометрически определяет некоторую кривую, называемую нтегральной кривой. Общее решение
геометрически определяет некоторую кривую, называемую нтегральной кривой. Общее решение 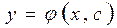 , определяет множество (семейство) всех интегральных кривых(рис.13.1).
, определяет множество (семейство) всех интегральных кривых(рис.13.1).
 Если требуется из семейства кривых выделить некоторую определенную кривую, необходимо задать дополнительные условия. Для этого достаточно указать точку плоскости Мо (x0 , y0), через которую проходит искомая интегральная кривая. Эти дополнительные условия называют начальными условиями. Обычно, их записывают в виде
Если требуется из семейства кривых выделить некоторую определенную кривую, необходимо задать дополнительные условия. Для этого достаточно указать точку плоскости Мо (x0 , y0), через которую проходит искомая интегральная кривая. Эти дополнительные условия называют начальными условиями. Обычно, их записывают в виде 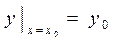 . Подставив координаты точки Мо в найденное общее решение, получаем
. Подставив координаты точки Мо в найденное общее решение, получаем 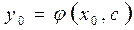 . Отсюда
. Отсюда 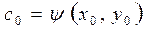 , а искомое частное решение имеет вид
, а искомое частное решение имеет вид 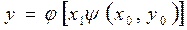 .Эта функция определяет искомую интегральную кривую.
.Эта функция определяет искомую интегральную кривую.
Пример. Дано дифференциальное уравнение 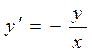 . Покажем, что его решением является функция
. Покажем, что его решением является функция 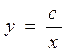 . Действительно
. Действительно  подставляем y и y' в заданное уравнение
подставляем y и y' в заданное уравнение  . Получено тождество.
. Получено тождество.
|
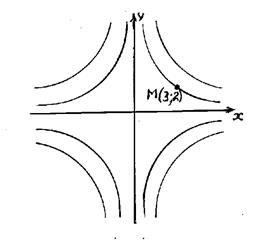
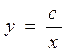 определяет множество гипербол (рис.13.2). Выделим ту из них, которая проходит через точку Мо (3 , 2). Подставим координаты точки Мо в общее решение
определяет множество гипербол (рис.13.2). Выделим ту из них, которая проходит через точку Мо (3 , 2). Подставим координаты точки Мо в общее решение 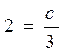 , тогда C = 6. Искомое частное решение
, тогда C = 6. Искомое частное решение 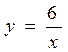 - эта функция определяет гиперболу, проходящую через точку Мо (3 , 2).
- эта функция определяет гиперболу, проходящую через точку Мо (3 , 2).
Замечание. Если решение дифференциального уравнения найдено в неявном виде 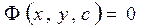 его называют общим интегралом.
его называют общим интегралом.
Задача Коши.
Рассмотрим уравнение.
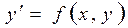 (13.6)
(13.6)
 Пусть функция
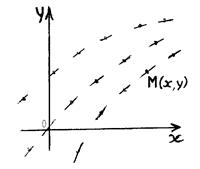
Пусть функция 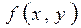 определена в области D плоскости xOy. Очевидно, уравнение (13.6) ставит всякой точке М (x , y) определенное значение производной y' , то есть определяет в точке М (x , y) угловой коэффициент касательной
определена в области D плоскости xOy. Очевидно, уравнение (13.6) ставит всякой точке М (x , y) определенное значение производной y' , то есть определяет в точке М (x , y) угловой коэффициент касательной 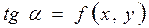 к интегральной кривой, проходящей через эту точку. Можно сказать, что уравнение (13.6) определяет совокупность направлений или поле направлений на плоскости xOy (рис.13.3).
к интегральной кривой, проходящей через эту точку. Можно сказать, что уравнение (13.6) определяет совокупность направлений или поле направлений на плоскости xOy (рис.13.3).
Таким образом, решение дифференциального уравнения (13.6), разрешенного относительно производной, сводится к отысканию кривых, направления касательных к которым в каждой точке плоскости совпадают с полем направлений.
Задача отыскания частного решения дифференциального уравнения 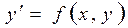 , разрешенного относительно производной, удовлетворяющего начальному условию
, разрешенного относительно производной, удовлетворяющего начальному условию 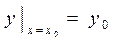 называется задачей Коши. Существование и единственность решения задачи Коши утверждается следующей теоремой:
называется задачей Коши. Существование и единственность решения задачи Коши утверждается следующей теоремой:
 Теорема. Пусть в дифференциальном уравнении
Теорема. Пусть в дифференциальном уравнении 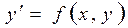 функция
функция 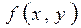 непрерывна и имеет непрерывную частную производную по y точке
непрерывна и имеет непрерывную частную производную по y точке 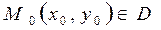 плоскости xOy. Тогда существует, причем единственное, решение
плоскости xOy. Тогда существует, причем единственное, решение 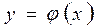 этого уравнения, такое, что
этого уравнения, такое, что  . Геометрически это означает, что через каждую точку
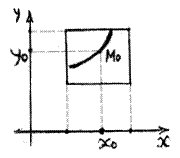
. Геометрически это означает, что через каждую точку 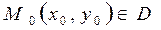 . проходит одна и только одна интегральная кривая (рис.13.4.).
. проходит одна и только одна интегральная кривая (рис.13.4.).

Дата добавления: 2015-11-06; просмотров: 1508;
