Однородные дифференциальные уравнения 1-го порядка.
 Определение. Функция
Определение. Функция  называется однородной порядка k , если для произвольного числа
называется однородной порядка k , если для произвольного числа 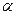 выполняется условие
выполняется условие 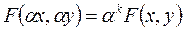 .
.
Примеры. Являются ли однородными следующие функции:
1. 
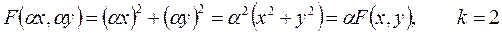
2. 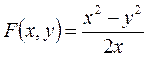
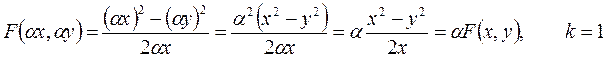 3.
3. 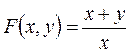
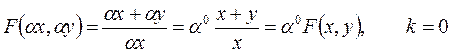
Отметим: если функция после замены x через αx и y через αy - не изменилась, то она является однородной порядка k=0.
4. 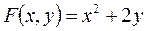
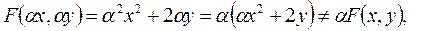 - функция не является однородной.
- функция не является однородной.
 Определение. Дифференциальное уравнение
Определение. Дифференциальное уравнение 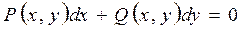 (13.8) называется однородным, если функция
(13.8) называется однородным, если функция  и
и 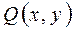 являются однородными одинакового порядка.
являются однородными одинакового порядка.
Пусть функции  и
и 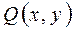 одинакового порядка k. Это означает, что
одинакового порядка k. Это означает, что 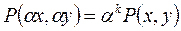 и
и 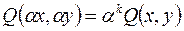 для любого
для любого 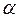 . Рассмотрим выражение
. Рассмотрим выражение
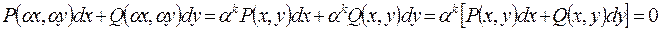
Согласно (13.8) это означает: если дифференцированное уравнение является однородным, то после замены в нем x через 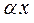 и y через
и y через 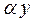 ононе изменяется. Этот вывод может служить критерием проверки дифференциального уравнения на однородность.
ононе изменяется. Этот вывод может служить критерием проверки дифференциального уравнения на однородность.
Можно использовать и дугой критерий. Пусть уравнение (13.8) однородное, и примем 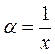 . Тогда
. Тогда

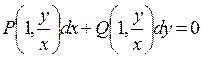 , отсюда
, отсюда 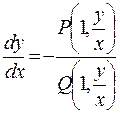
Обозначим 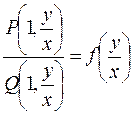
Функция 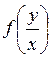 является однородной нулевого порядка (k=0), а однородное дифференциальное уравнение (13.8) может быть записано в виде
является однородной нулевого порядка (k=0), а однородное дифференциальное уравнение (13.8) может быть записано в виде
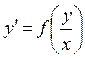 или
или 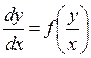 (13.9)
(13.9)
Покажем, что введение вспомогательной переменной 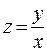 позволяет свести однородное уравнение (13.8) (или 13.9) к дифференциальному уравнению с разделяющимися переменными. Очевидно,
позволяет свести однородное уравнение (13.8) (или 13.9) к дифференциальному уравнению с разделяющимися переменными. Очевидно, 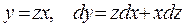
Перейдем в уравнении (13.8) к новой переменной z. Полагая 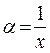 запишем уравнение (13.8), как было показано выше, в виде
запишем уравнение (13.8), как было показано выше, в виде
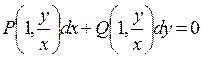 , так как
, так как 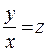 , получаем
, получаем
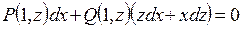
После преобразования имеем 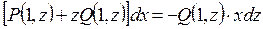
Это уравнение с разделяющимися переменными, которое можно записать в виде
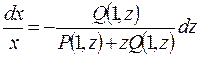
Его общее решение имеет вид
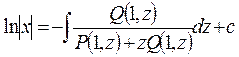
Пример. Найти решение дифференциального уравнения
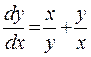
Функция 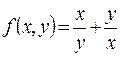 - однородная нулевого порядка. Введем вспомогательную переменную
- однородная нулевого порядка. Введем вспомогательную переменную 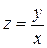 (
( 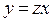 ). Данное уравнение примет вид
). Данное уравнение примет вид 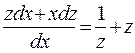 , или
, или  .
.
После преобразования получаем уравнение 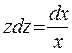 с разделенными переменными. Проинтегрируем его.
с разделенными переменными. Проинтегрируем его. 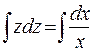 , откуда
, откуда 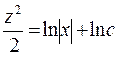 или
или 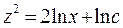 . Возвращаясь к исходным переменным, запишем общее решение
. Возвращаясь к исходным переменным, запишем общее решение
 или
или 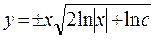
Дата добавления: 2015-11-06; просмотров: 903;
