Смешанное произведение в координатной форме.
Возьмем три вектора в координатной форме:
а= (ах, ау, аz)= axi + ayj + azk;
b= (bx, by, bz)= bxi + byj + bzk;
с= (сx, сy, сz) = cxi + cyj + czk.
abc= (a´b)• с.
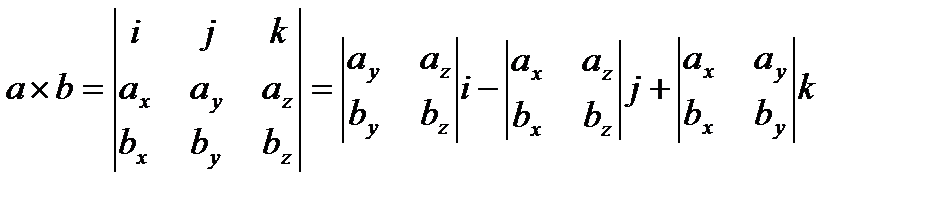
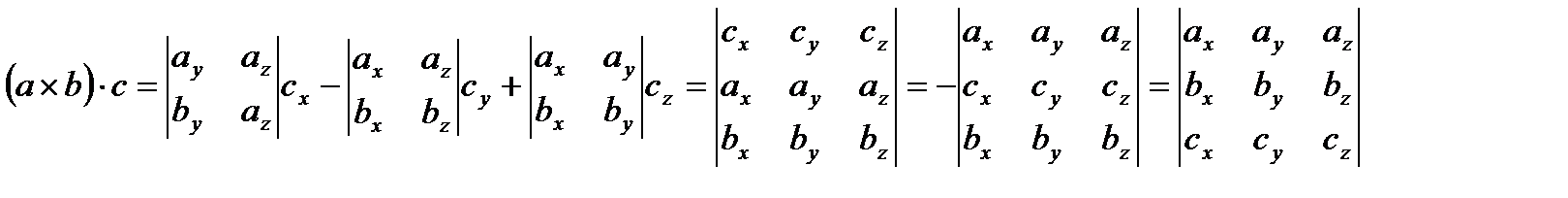
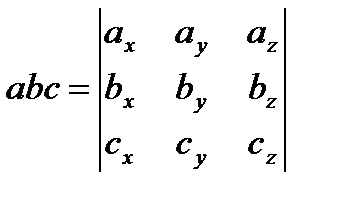 .
.
Приложения смешанного произведения.
1) Модуль смешанного произведения численно равен объему параллелепипеда, построенного на трех векторах как на ребрах.
Vпарал= │abc│.
Из геометрии: Vпарал= Sосн· h.
Sосн= Sпар=│a´b│.
Из приложения векторного произведения:
h=│с│·cos φ.
Vпарал= │ a´b │·│c│·cos φ =│(a´b) • с│=│abc│.
Следствие: высота параллелепипеда h= 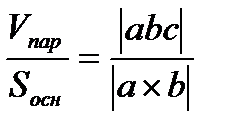 .
.
2) Vтетр=  Vпарал=
Vпарал=  │abc│.
│abc│.
Из геометрии: Vтетр= 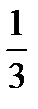 Sосн· h; hтетр=
Sосн· h; hтетр= 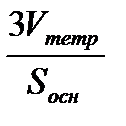 .
.
3) Если смешанное произведение abc>0, то тройка векторов правая; если abc<0, то тройка векторов левая.
abc= (a´b) • с = │a´b│·│c│·cos φ.
abc>0, cos φ >0, Ðj- острый, abc - правая тройка.
abc<0, cos φ <0, Ðj- тупой, abc - левая тройка.
4) abc – компланарные, если параллельны одной плоскости или лежат в одной плоскости.
Условие компланарности: abc=0.
a´b ^ плоскости α.
a´b ^ с, (a´b) • с = 0 (условие перпендикулярности двух векторов), abc=0.
Дата добавления: 2015-11-06; просмотров: 3317;
