Сфера в пространстве.
Определение: Сферой называют множество точек пространства, равноудаленных от заданной точки (центр сферы) на заданное расстояние (радиус сферы).
Пусть центр сферы С(a, b, c), радиус R, т. М (х, у, z) - текущая точка сферы.
По определению: │СМ│= R.
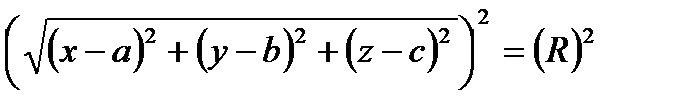
| M(x, y, z) |
| y |
| z |
| х |
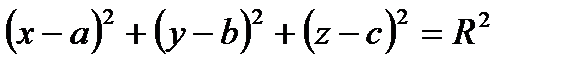 - нормальное уравнение сферы.
- нормальное уравнение сферы.
Если центра сферы - О(0, 0, 0), тогда
x2+ y2+ z2= R2 - каноническое уравнение сферы.
Замечание:
В пространстве различают поверхности двух видов:
1) поверхности первого порядка Ax+ By+ Cz+ D= 0 (уравнение плоскости)
2) поверхности второго порядка
Ax2+ By2+ Cz2+ 2Dxy+ 2Fyz+ Kx+ My+ Nz+ L= 0.
Примером поверхности второго порядка служит сфера, остальные поверхности второго порядка: цилиндры, конусы, параболы и другие.
| Скалярное произведение | Векторное произведение | Смешанное произведение |
| Определение | ||
| число а•b=│а│·│b│cos φ | a´b= вектор с, что 1° │с│=│a│·│b│sin φ, где Ðj= a,b 2° вектор c^a, c^b, т.е. с ^ плоскости, в которой лежат вектора а и b. 3° кратчайший поворот от вектора a к b, видимый с конца вектора с будет против часовой стрелки. | число аbc= (a´b) • с |
| Свойства | ||
| 1° a • b = b • a 2° a • b= 0, т.к. a ┴ b 3° (λa)• b= λ(a• b) 4° a•(b + c)= a• b + a• c 5° а • а= │a│2 | 1° антикоммунитативность a´b= -b´a 2° (λa)´b= λ (a´b) 3° a´(b + с)= a´b + a´с 4° a ´ а= 0 | 1° abc= - bac= bca= ... 2° (λa)bc= λ(abc) 3° (a+ b) cd= acd+ bcd 4° ijk= (i×j)· k= k· k= │k│2= 1 ijk= 1 |
| Вычисление в координатной форме | ||
| a•b= ax bx + ay by + az bz | 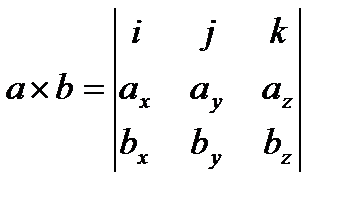
| 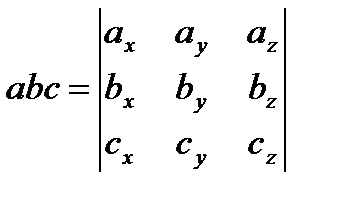
|
| Приложения | ||
1) 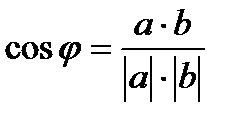 2)Ðj - острый, cosj>0, отсюда следует: a•b> 0.
Ðj - тупой, cosj<0, отсюда следует: a•b< 0.
Ðj=90°, cosj=0,
отсюда следует: a•b= 0.
3)
2)Ðj - острый, cosj>0, отсюда следует: a•b> 0.
Ðj - тупой, cosj<0, отсюда следует: a•b< 0.
Ðj=90°, cosj=0,
отсюда следует: a•b= 0.
3)
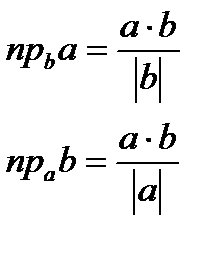
| 1) Sпар=│a ´ b│
2) 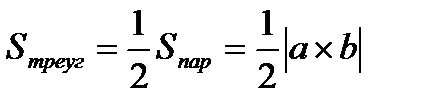 3) a║b, отсюда следует, что
│ a´b│= 0.
3) a║b, отсюда следует, что
│ a´b│= 0.
| 1) Vпарал= │abc│
2) Vтетр= 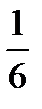 Vпарал
Vтетр = Vпарал
Vтетр = 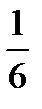 │abc│
3) если abc>0, то тройка векторов правая; если abc<0, то тройка векторов левая.
4) abc – компланарные: abc=0. │abc│
3) если abc>0, то тройка векторов правая; если abc<0, то тройка векторов левая.
4) abc – компланарные: abc=0.
|
Дата добавления: 2015-11-06; просмотров: 716;
