Расстояния между различными объектами в пространстве.
1) Расстояние от точки до плоскости.
Найдем расстояние от т. М0 (x0, y0, z0) до плоскости Ax+By+Cz+D=0. Расстояние от точки до плоскости - это длина перпендикуляра, опущенного из точки на плоскость. Проведем через М0 прямую, перпендикулярную плоскости. т. N0 – точка пересечения прямой и плоскости.
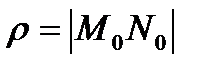 .
.
а) Составим параметрические уравнения прямой:
l= N= (A, B, C) ║прямой,
т. М0 (x0, y0, z0) Є прямой.
x= At+ x0
y= Bt+ y0.
z= Ct+ z0
б) т. N0 – общая для прямой и плоскости, поэтому подставим параметрические уравнения прямой в уравнение плоскости и найдем параметр, соответствующий т. N0:
A(At+ x0) + B(Bt+ y0) + C(Ct+ z0) + D=0;
(A2+ B2+ C2)t+ Ax0+ By0+ Cz0+ D=0;
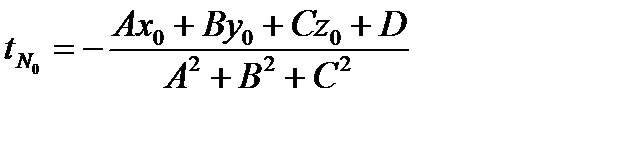 ,
,
координаты т. N0 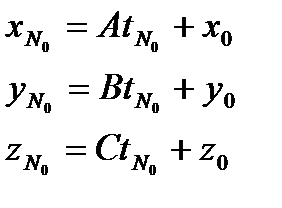 .
.
в)

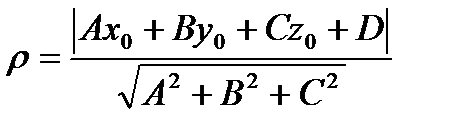 - расстояние от точки до плоскости.
- расстояние от точки до плоскости.
2) Расстояние между двумя параллельными плоскостями.
На одной плоскости нужно взять произвольную точку и найти расстояние от этой точки до другой плоскости.
3) Расстояние между прямой и параллельной плоскостью.
На прямой нужно взять произвольную точку и найти расстояние от этой точки до плоскости.
| а |
| α |
4) Расстояние от точки до прямой.
т. М0 (3, 1, -1), прямая 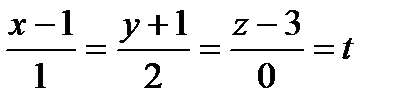 .
.
M0
N0
a
l
ρ
Проведем через т. М0 плоскость, перпендикулярную прямой (проектирующая плоскость). Найдем точку пересечения прямой и плоскости.
 .
.
а) Составим уравнение плоскости:
l= N= (1, 2, 0) ^ плоскости,
т. М0 (3, 1, -1) Є плоскости.
A(x- x0) + B(y- y0) + C(z- z0)= 0,
1(x- 3) + 2(y- 1) + 0(z+ 1)= 0,
x+ 2y- 5= 0 - уравнение плоскости.
б) Составим параметрические уравнения прямой:
x= t+ 1
y= 2t- 1
z= 0t- 3
в) т. N0 – точка пересечения прямой и плоскости. Подставим параметрические уравнения прямой в уравнение плоскости.
(t+ 1)+ 2(2t- 1)- 5= 0, t+ 1+ 4t- 2- 5= 0, 5t- 6= 0, 5t= 6.
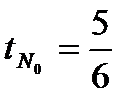 , т. N0
, т. N0 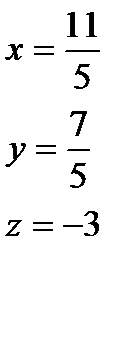
т. N0 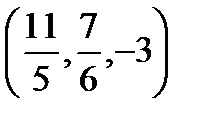 .
.
г) 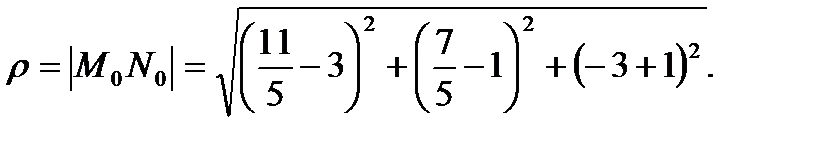
Дата добавления: 2015-11-06; просмотров: 1039;
