Відношення порядку на множині дійсних чисел.

3. Перед тим як розглянути дії над дійсними числами потрібно навчитися їх порівнювати, причому правила порівняння повинні включати в себе правила порівняння раціональних чисел. Оскільки кожне дійсне число можна представити у вигляді десяткового дробу, то було б доцільно порівнювати дійсні числа як порівнюються десяткові дроби.

Означення: два додатних дійсних числа називаються рівними, якщо в їхніх зображеннях за допомогою нескінченного неперіодичного десяткового дробу збігаються як цілі частини, так і всі десяткові знаки вправо від коми.

Означення:із двох додатних дійсних чисел більшим (меншим) буде те, у якого більша (менша) ціла частина, а якщо цілі частини рівні, то більшим (меншим) буде те, у якого більшим (меншим) буде перший із нерівних десяткових знаків.

Так само, як і при порівнянні від’ємних раціональних чисел, для порівняння від’ємних дійсних чисел введемо поняття модуля дійсного числа.

Означення:модулем дійсного числа α називають відстань від початку відліку числової прямої до точки цієї прямої, яка зображає число α.

Інколи означення модуля дійсного числа α дають в такій символічній формі:

α, якщо α≥0,

│α│=

Якщо α<0.

Вправа: Знайдіть модулі чисел: -12; 4; -3,5; 0; -2 .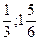

Розв’язання.

Відповідно до вищенаведеного означення маємо: │-12│=-(-12)=12, бо -12<0; │4│=4, бо 4>0; │-3,5│= -(-3,5)=3,5, бо -3,5<0;│0│=0; │-2⅓│= -(-2⅓)=2⅓.

Означення: із двох від'ємних дійсних чисел більшим (меншим) буде те, модуль якого менший (більший).

Вправа: порівняти пари дійсних чисел: -Ö6 і -Ö7; -Ö12 і -Ö15.

Розв’язання.

Оскільки │-Ö6│=Ö6 і │-Ö7│=Ö7, а Ö6<Ö7, тобто │-Ö6│<│-Ö7│, то -Ö6>-Ö7. Аналогічно пропонуємо розв’язати друге завдання.

Якщо зобразити кожне дійсне число точкою числової прямої, то можна прийняти таке правило порівняння дійсних чисел:

Правило: із двох дійсних чисел більшим (меншим) буде те, яке зображається правіше (лівіше) на числовій прямій.