Додавання і віднімання невід’ємних раціональних чисел. Теореми про існування та єдиність суми і різниці. Властивості (закони) додавання.
5. Однією з умов розширення множини цілих чисел була вимога про необхідність збереження сутності та правил виконання операцій над цілими числами в новій числовій множині. Саме тому, будемо визначати операції над невід’ємними раціональними числами так, щоб це не суперечило правилам виконання цих операцій у попередній числовій множині. Для цього, як ми вже зазначали, кожне ціле число будемо розглядати як дріб із знаменником 1. Оскільки 1+2=3, тобто 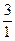 , то
, то 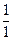 +
+ 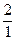 =
= 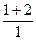 =
= 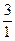 . Саме тому доцільно прийняти таке означення.
. Саме тому доцільно прийняти таке означення.
Означення: сумою двох дробових чисел з однаковими знаменниками є дробове число, чисельник якого дорівнює сумі чисельників, а знаменник – дорівнює їх спільному знаменнику.
Наприклад, 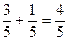 . Прийняте означення можна поширити на будь-яку скінченну кількість доданків, наприклад:
. Прийняте означення можна поширити на будь-яку скінченну кількість доданків, наприклад: 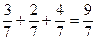 . Як же бути в тому випадку, коли дроби мають різні знаменники? – звести їх до спільного знаменника і додати за попереднім означенням. Можна прийняти і наступне означення.
. Як же бути в тому випадку, коли дроби мають різні знаменники? – звести їх до спільного знаменника і додати за попереднім означенням. Можна прийняти і наступне означення.
Означення: сумою двох невід’ємних раціональних чисел 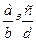 називається третє невід’ємне раціональне число
називається третє невід’ємне раціональне число 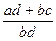 , тобто
, тобто 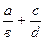 =
= 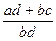 .
.
У жодному з означень нічого не говориться про існування та єдиність суми невід’ємних раціональних чисел. Саме тому слід довести відповідні теореми.
Теорема: сума невід’ємних раціональних чисел існує і єдина.
Доведення.
Розглянемо два дроби 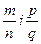 такі, що m і р єZ0, а n і qєN. Знайдемо їх суму.
такі, що m і р єZ0, а n і qєN. Знайдемо їх суму. 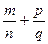 =
= 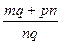 - згідно означення. Тоді mqÎZ0, pnÎZ0 і nqÎZ0, а тому одержаний нами дріб
- згідно означення. Тоді mqÎZ0, pnÎZ0 і nqÎZ0, а тому одержаний нами дріб 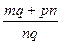 - існує і єдиний. Теорему доведено.
- існує і єдиний. Теорему доведено.
Для того, щоб одержати відповідь на запитання: «чи підкоряється операція додавання невід’ємних раціональних чисел комутативному та асоціативному законам?», необхідно довести відповідні теореми.
Теорема: операція додавання в множині невід’ємних раціональних чисел підкоряється комутативному та асоціативному законам.
Символічно вони запишуться так: (" 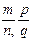 єQ0)(
єQ0)( 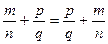 ); ("
); (" 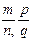 ,
, 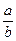 єQ0)((
єQ0)(( 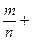
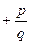 )+
)+ 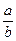 =
= 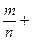 (
( 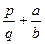 )).
)).
Доведення.
Розглянемо три дробових числа, але для спрощення викладок виберемо їх із спільними знаменниками, 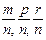 і доведемо, що (
і доведемо, що ( 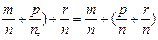 ). (
). ( 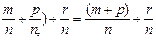 =(Чому?!)=
=(Чому?!)= 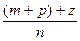 (Чому?!)=
(Чому?!)= 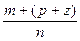 (Чому?!)=
(Чому?!)= 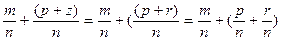 . Отже, (
. Отже, ( 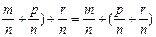 ) сполучний закон додавання невід’ємних раціональних чисел доведено.
) сполучний закон додавання невід’ємних раціональних чисел доведено.
Означення: сума натурального числа і дробового числа, записаних поряд без знака додавання називають мішаним числом.
Наприклад, 8+ 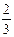 =8
=8 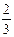 . Щоб представити мішане число дробовим, його необхідно перетворити у неправильний дріб, а саме: 8
. Щоб представити мішане число дробовим, його необхідно перетворити у неправильний дріб, а саме: 8 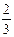 =
= 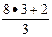 =
= 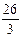 . Щоб перетворити неправильний дріб у мішане число, потрібно поділити чисельник на знаменник і частку записати перед дробом, а остачу записати у чисельнику, залишивши той самий знаменник, наприклад:
. Щоб перетворити неправильний дріб у мішане число, потрібно поділити чисельник на знаменник і частку записати перед дробом, а остачу записати у чисельнику, залишивши той самий знаменник, наприклад: 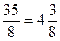 . Отже, множина невід’ємних раціональних чисел замкнена відносно операції додавання.
. Отже, множина невід’ємних раціональних чисел замкнена відносно операції додавання.
Операцію віднімання у множині невід’ємних раціональних чисел також означатимемо так, щоб це не суперечило правилам віднімання цілих чисел.
Означення: відняти від дробового числа  дробове число
дробове число 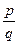 - це означає знайти таке дробове число
- це означає знайти таке дробове число  -
- 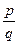 , яке у сумі з дробовим числом
, яке у сумі з дробовим числом 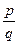 дає нам дробове число
дає нам дробове число  .
.
Таке означення не суперечить тому, яке ми прийняли для невід’ємних цілих чисел. Для того, щоб знайти різницю двох дробових чисел, приймемо наступне означення.
Означення: різницею двох дробових чисел з рівними знаменниками називається таке третє дробове число, чисельник якого дорівнює різниці чисельників, а знаменник – спільному знаменнику.
Символічно прийняте означення запишеться так:  -
- 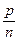 =
= 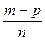 . Щоб знайти різницю дробових чисел з різними знаменниками, слід звести їх до спільного знаменника та використати попереднє означення. Символічно це запишеться так:
. Щоб знайти різницю дробових чисел з різними знаменниками, слід звести їх до спільного знаменника та використати попереднє означення. Символічно це запишеться так:  -
- 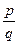 =
= 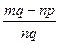 . У прийнятих означеннях нічого не говориться про існування та єдиність різниці. Саме тому слід довести наступні теореми.
. У прийнятих означеннях нічого не говориться про існування та єдиність різниці. Саме тому слід довести наступні теореми.
Теорема: різниця двох невід’ємних раціональних чисел  і
і 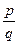 існує тоді і тільки тоді, коли
існує тоді і тільки тоді, коли  ³
³ 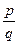 .
.
Доведення.
Для спрощення викладок розглядатимемо дроби з однаковими знаменниками. Оскільки у формулюванні теореми є словосполучення «тоді і тільки тоді», то доведення складатиметься з двох частин: 1) якщо різниця  -
- 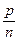 існує, то
існує, то  ³
³ 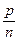 ; 2) якщо
; 2) якщо  ³
³ 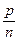 , то різниця
, то різниця  -
- 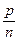 існує.
існує.
Доведемо першу частину. Оскільки різниця  -
- 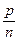 існує, то маємо
існує, то маємо 
 -
- 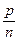 =
= 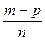 , де m³p, а тому
, де m³p, а тому  ³
³ 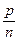 (Чому?!). Першу частину доведено. Для доведення другої частини використаємо те, що
(Чому?!). Першу частину доведено. Для доведення другої частини використаємо те, що  ³
³ 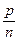 . Оскільки
. Оскільки  ³
³ 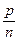 , то різниця
, то різниця  -
- 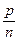 - додатна, а тоді
- додатна, а тоді  -
- 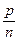 =
= 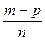 - також додатна. Це означає, що m-p³0. Отже, число m-p належить множині Z0. Таким чином, різниця
- також додатна. Це означає, що m-p³0. Отже, число m-p належить множині Z0. Таким чином, різниця  -
- 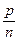 існує. Теорему доведено повністю.
існує. Теорему доведено повністю.
Теорема: якщо різниця невід’ємних раціональних чисел існує, то вона єдина.
Доведення цієї теореми пропонуємо провести методом від супротивного самостійно.
Дата добавления: 2015-11-04; просмотров: 1841;
