Невід’ємні раціональні числа та їх властивості.

3. Розширюючи множину цілих чисел, ми зазначали, що у новій числовій множині цілі числа повинні зберегтися. Для цього кожне ціле число буде позначати дробовим числом із знаменником 1. Наприклад, 0= 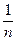, 1= , 2= 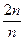тощо, де n – довільне ціле число. Тепер всі дроби можна розбити на класи, до кожного з яких входитимуть рівносильні дроби. Так, до першого класу віднесемо всі дроби рівносильні числу 0, до другого – рівносильні числу 1, тобто 1, 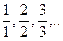, до наступного дроби, які дорівнюють 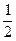, тобто 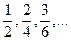, тощо. Всі дроби кожного класу визначають одне й те ж саме дробове число. Серед множини цих чисел є одне особливе. Це нескоротний дріб.

Означення: додатнім раціональним числом називається множина рівносильних йому дробів { , , , …, , …}.

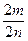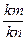Так, наприклад дробовим числом є множина рівносильних дробів , дробовим числом є множина рівносильних дробів 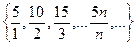. У математиці доведено теорему, яку ми приймемо без доведення і яка вказує на існування та єдиність такого дробу.

Теорема: для будь-якого додатного раціонального числа існує один і тільки один дріб, що його представляє, й такий, що чисельник і знаменник його взаємно-прості числа.

Означення: об’єднання множини невід’ємних цілих чисел та додатних дробів називають множиною невід’ємних раціональних чисел.

Символічно ця множина позначається так Q₀. Перейдемо до розгляду властивостей цієї множини. Цілком зрозуміло, що в множині додатних раціональних чисел повинні зберегтися деякі властивості, що були в множині цілих чисел. Крім того, ця нова числова множина повинна мати і нові властивості, яких не було в попередній числовій множині.

Означення: числова множина називається щільною в собі, якщо між будь-якими її двома елементами міститься безліч елементів цієї множини.

Теорема:множина невід'ємних раціональних чисел щільна в собі.

Доведення.

Нехай а,bÎQ₀. Приймемо, що a<b. Нехай додамо до обох частин 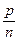. Тоді матимемо 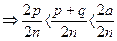. Позначимо 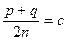, тоді a<c<b. Отже, ми показали, що між додатними раціональними числами а і b є ще одне додатне раціональне число. Аналогічно можна довести, що і між числами а і с та с і b є додатні раціональні числа. Таким чином, теорему доведено.

Розглядаючи властивості множини цілих чисел, ми ввели поняття зчисленної множини, як множини, яка еквівалентна множині натуральних чисел. Покажемо, що і множина невід’ємних раціональних чисел має цю властивість, тобто є зчисленною.

Теорема: множина Q₀ невід’ємних раціональних чисел зчисленна.

Доведення.

Для доведення теореми слід показати, що між елементами множини невід’ємних раціональних чисел і множини натуральних чисел можна встановити взаємно однозначну відповідність. Подамо кожне невід’ємне раціональне число нескоротним дробом. Назвемо висотою нескоротного дробу суму його чисельника і знаменника. Впорядкуємо всі нескоротні дроби в порядку зростання висоти, а при однаковій висоті будемо розміщати їх в порядку зростання чисельників. Нехай дробу відповідає натуральне число 1, дробові 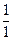– натуральне число 2, дробовому числу 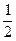- натуральне число 3 тощо. Таким чином, маємо: 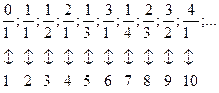Що й треба було довести.

З іншими властивостями множини невід’ємних раціональних чисел будемо знайомитися в процесі розгляду іншого матеріалу.